平成22年度・秋田県(数学)高校入試問題 [平成22年度(2010年)・数学]
平成22年度・秋田県(数学)高校入試問題のダウンロードはこちらから
http://www.pref.akita.lg.jp/icity/browser?ActionCode=genlist&GenreID=1137480909413
■■まとめ■■
かなり難しい問題です。しっかりと勉強しておかないと得点奪取は難しいでしょう。
問題量も多いので,計算力も問われます。
★★つきは1つ用意しました。
[5]は折り曲げに関する問題で,三平方の定理を多用します。
この3つの問題を解けるようになれば,色々なパターンの折り曲げに関する問題に対応できるようになりますので,3問ともぜひ見ておきましょう。
■■ポイント■■
[1]高校によって採択する問題が異なる。
(1)①積が最も大きいのは2と4のペア。②積が最も小さいのは-3と4のペア
(2)イはアの5/2倍であるから,①15 ②5a/2
(3)(4)は計算問題。
(5)3m=2a+bだから,b=3m-2a
(6)下式より,y=9+3xを上式に代入して,
x+2(3x+9)=4 → 7x=-14 → x=-2
これを下式に代入してy=3。(x,y)=(-2,3)
(7)(x+4)(x-4)=3x-6
x^2-16-3x+6=0 → x^2-3x-10=0
→ (x-5)(x+2)=0 → x=5,-2
(8) a=5b+rである。よって,r=a-5b
(9)方程式の持つ意味である。毎分160mで走った距離を表す。
(10)A=10x+yとすると,B=10y+xとなる。
A+B=11x+11y=11(x+y)
A-B=9x-9y=9(x-y) となる。
よって,x+yが11であり,x-yが平方数になっていなければならない。このとき,x=6,y=5のとき
である。よって,A=65
(11)∠ABC=70°であり,△ABCは二等辺三角形なので,∠A=40°。弧BCに対する円周角は等しいの
で,∠x=40°
(12)中点連結定理を何回か使う。GE=3→FC=6。
DH:HC=DG:FC=1:3よりDG=2。よって,再び中点連結定理より,BC=4(cm)
(13)AB//CDで錯角の関係より,∠BEC=∠ECDから,△BECは二等辺三角形である。
よって∠ECB=52°で∠B=180-52×2=76°。よって∠x=76°
(14)底面積は正方形の半分の面積である。
よって,V=6×6÷2×6÷3=36(cm3)
(15)PとQでは,
①下の底面積は同じ。
②上の底面積は半径3cmの円と,回転軸から3cm離れたドーナツ型の部分はやはり同じ。
③立体Pで,上の部分の側面積は6π×3=18π
立体Pで,下の部分の側面積は12π×3=36π
立体Qで,内側部分の側面積は6π×3=18π
立体Qで,外側部分の側面積は,12π×6=72π。
立体Qの方は36πだけ大きい。
[2]関数・グラフの見方・考え方に関する問い。
(1)[a]ウ[b]ア[c]エ。会話を読んで判断する。[d]大きく
会話の内容が理解できただろうか。
(2)[ア]12分後。これはグラフを見て考える。
[イ][ウ]美咲さんは高さ6cmでグラフの傾きがかわり,健司さんは8cmでグラフの傾きがかわった
ので,a=6cm,b=8cm
[エ]上記より,8cmのところから高さが等しくなる。
[オ]水面が等しくなってからは,同じ関数の式で表される。傾き1/2で,(4,6)を通るので,
y=1/2x+4
(3)この場合は(2)のグラフから(12,10)で終わるような比例のグラフを書けばよい。
y=5x/6のグラフを書く。(グラフ略)
[3]円と証明や作図に関する問題
(1)√2と言う数字を見たときに何を思い浮かべるかである。これは45°定規の斜辺を考えたら
よいだろう。
①数直線1から垂線を立てる。
②その垂線上に「1」の長さを取る。
③対角線は であるから,その長さを数直線上にとる,という3段階の作図をすればよい。
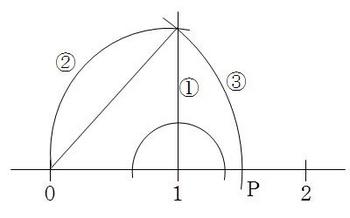
(2)弦の長さが等しければ,弧の長さも等しくなるという知識を問う問題である。
△APBと△AQBにおいて,
AP=AQ(仮定) AB=AB(共通)
∠APB=∠AQB=90°(半円の弧に対する円周角)
よって直角三角形で斜辺と他の1辺がそれぞれ等しいので,△APB≡△AQB。
対応する核の大きさが等しいので∠PAB=∠QAB。
これは線分ABが∠PAQを二等分していることを表している。
[4]2次関数と確率の問題
(1)①関数の変域の問題は必ずグラフを書きながら行う。今回は原点を通過するので,
x=-1のときは考えなくてよい。x=3のときy=18であるから,0≦y≦18
②Cのx座標をtとすると,C(t,1/2t^2) ,A(t,2t^2)となるので,Aのy座標は4倍である。
③BCの長さは2t,ACの長さは3t^2/2であるから,2BC=AC → 4t=3t^2/2。これを解くとt=8/3と
なるので,Bのx座標は-8/3
(2)①2枚のカードを同時に取り出すので,組合せの考え方を使う。全部の場合の数は6通り。
そのうち,12以下になるのは,(1,3),(1,6),(1,10),(3,6)の4通りあるので,2/3
②3枚取り出したとき12以下となる場合が2通りしかない場合は次のように考える。
[1]まずxを使わない 1+3+6=10で一通りは必ずこれになる。
[2]xを使う 1+3+x=4+xが12以下でなくてはならず,
1+6+x=7+xは12より大きくなければならない。
これを考えると,x=8,7のみである。
[5]選択問題:学校によって採択が異なりますが,全て折り曲げの問題です。
[Ⅰ](1)①∠EDC=60°
②Dから垂線を下ろせば,△DECと同じ形の図形が現れることがわかる。よって△DCEの4倍である。
(2)BG=xとすると,AG=x,GC=6√3-xであるから,
△BGCで三平方の定理より,x^2=(6√3-x)^2+6^2 x=4√3
[Ⅱ](1)折り曲げた図形があるので,同じ角度の部分がたくさんできる。
四角形DGECは台形であるから,
∠DGE+∠GEC=180°。∠DGF=38°,∠FGE=90°であるから,∠GEC=52°
よって∠GEFはその半分であるから,26°
(2)JIB=60°,∠JIC=120°であるから,∠JIH=∠HIC=60°となる。
錯角から∠IJH=60°で△JIHは正三角形になる。JからBCに垂線を下ろすと,
JI=6√3であることがわかる。△JHKも30°の三角定規の形であるから,KH=3√3
(3)まず,△ANMはAN=AMの二等辺三角形である。
①∠ANM=∠CNM(折り曲げたから)
②∠CNM=∠NMA(平行線の錯角) であるので
∠ANM=∠NMAで二等辺三角形である。
この三角形の面積はAMを底辺として高さをCDとする。
AN=xとすると,NC=x,BN=12-xであるから,△ABNで三平方の定理より,
6^2+(12-x)^2=^x2 → 36+144-24x=0
よって△AMN=15/2×6÷2=45/2(cm2)
[Ⅲ](1)この図ではNCのちょうど2倍がECになっているので,△ENCが30°の三角定規の形になっている。
よって∠ECD=30°,∠ECF=15°であるから,△FECの内角の和を考えて,∠EFC=75°
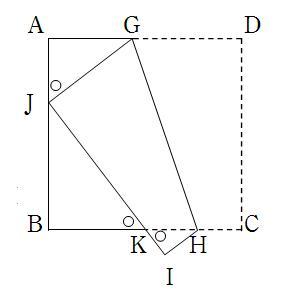
(2)AB=9,AG=4から,
DG=JG=5。△AJGで
3:4:5の三角形となる。
また,図のように等しい角度
を○とすると,△JBKも△KIH
も3:4:5の三角形になる。
JB=6から,JK=6×5/4=15/2。
KI=9-15/2=3/2で,IH=HC=3/2×4/3=2。
求める四角形GJIHの面積は四角形GDCHと等しいので,
(5+2)×9÷2=63/2
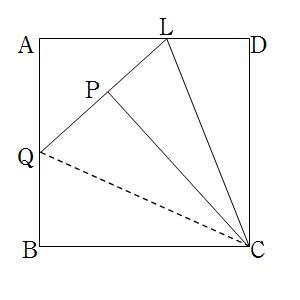
(3)図のようにCQを結ぶと
CP=CB(正方形の1辺)
CQは共通
∠CBQ=∠CPQ=90°
であるから,斜辺と他の1角が
それぞれ等しいので
△CBQ≡△CPQとなる。
AL=3,LD=2とすると,LP=2。QB=xとすると,AQ=5-xで,PQ=xより,
△ALQで三平方の定理より,
(5-x)^2+3^2=(2+x)^2 → 25-10x+x^2+9=4+4x+x^2
x=15/7→ より,AQ=20/7 。よって,AQはQBの4/3倍
http://www.pref.akita.lg.jp/icity/browser?ActionCode=genlist&GenreID=1137480909413
■■まとめ■■
かなり難しい問題です。しっかりと勉強しておかないと得点奪取は難しいでしょう。
問題量も多いので,計算力も問われます。
★★つきは1つ用意しました。
[5]は折り曲げに関する問題で,三平方の定理を多用します。
この3つの問題を解けるようになれば,色々なパターンの折り曲げに関する問題に対応できるようになりますので,3問ともぜひ見ておきましょう。
■■ポイント■■
[1]高校によって採択する問題が異なる。
(1)①積が最も大きいのは2と4のペア。②積が最も小さいのは-3と4のペア
(2)イはアの5/2倍であるから,①15 ②5a/2
(3)(4)は計算問題。
(5)3m=2a+bだから,b=3m-2a
(6)下式より,y=9+3xを上式に代入して,
x+2(3x+9)=4 → 7x=-14 → x=-2
これを下式に代入してy=3。(x,y)=(-2,3)
(7)(x+4)(x-4)=3x-6
x^2-16-3x+6=0 → x^2-3x-10=0
→ (x-5)(x+2)=0 → x=5,-2
(8) a=5b+rである。よって,r=a-5b
(9)方程式の持つ意味である。毎分160mで走った距離を表す。
(10)A=10x+yとすると,B=10y+xとなる。
A+B=11x+11y=11(x+y)
A-B=9x-9y=9(x-y) となる。
よって,x+yが11であり,x-yが平方数になっていなければならない。このとき,x=6,y=5のとき
である。よって,A=65
(11)∠ABC=70°であり,△ABCは二等辺三角形なので,∠A=40°。弧BCに対する円周角は等しいの
で,∠x=40°
(12)中点連結定理を何回か使う。GE=3→FC=6。
DH:HC=DG:FC=1:3よりDG=2。よって,再び中点連結定理より,BC=4(cm)
(13)AB//CDで錯角の関係より,∠BEC=∠ECDから,△BECは二等辺三角形である。
よって∠ECB=52°で∠B=180-52×2=76°。よって∠x=76°
(14)底面積は正方形の半分の面積である。
よって,V=6×6÷2×6÷3=36(cm3)
(15)PとQでは,
①下の底面積は同じ。
②上の底面積は半径3cmの円と,回転軸から3cm離れたドーナツ型の部分はやはり同じ。
③立体Pで,上の部分の側面積は6π×3=18π
立体Pで,下の部分の側面積は12π×3=36π
立体Qで,内側部分の側面積は6π×3=18π
立体Qで,外側部分の側面積は,12π×6=72π。
立体Qの方は36πだけ大きい。
[2]関数・グラフの見方・考え方に関する問い。
(1)[a]ウ[b]ア[c]エ。会話を読んで判断する。[d]大きく
会話の内容が理解できただろうか。
(2)[ア]12分後。これはグラフを見て考える。
[イ][ウ]美咲さんは高さ6cmでグラフの傾きがかわり,健司さんは8cmでグラフの傾きがかわった
ので,a=6cm,b=8cm
[エ]上記より,8cmのところから高さが等しくなる。
[オ]水面が等しくなってからは,同じ関数の式で表される。傾き1/2で,(4,6)を通るので,
y=1/2x+4
(3)この場合は(2)のグラフから(12,10)で終わるような比例のグラフを書けばよい。
y=5x/6のグラフを書く。(グラフ略)
[3]円と証明や作図に関する問題
(1)√2と言う数字を見たときに何を思い浮かべるかである。これは45°定規の斜辺を考えたら
よいだろう。
①数直線1から垂線を立てる。
②その垂線上に「1」の長さを取る。
③対角線は であるから,その長さを数直線上にとる,という3段階の作図をすればよい。
(2)弦の長さが等しければ,弧の長さも等しくなるという知識を問う問題である。
△APBと△AQBにおいて,
AP=AQ(仮定) AB=AB(共通)
∠APB=∠AQB=90°(半円の弧に対する円周角)
よって直角三角形で斜辺と他の1辺がそれぞれ等しいので,△APB≡△AQB。
対応する核の大きさが等しいので∠PAB=∠QAB。
これは線分ABが∠PAQを二等分していることを表している。
[4]2次関数と確率の問題
(1)①関数の変域の問題は必ずグラフを書きながら行う。今回は原点を通過するので,
x=-1のときは考えなくてよい。x=3のときy=18であるから,0≦y≦18
②Cのx座標をtとすると,C(t,1/2t^2) ,A(t,2t^2)となるので,Aのy座標は4倍である。
③BCの長さは2t,ACの長さは3t^2/2であるから,2BC=AC → 4t=3t^2/2。これを解くとt=8/3と
なるので,Bのx座標は-8/3
(2)①2枚のカードを同時に取り出すので,組合せの考え方を使う。全部の場合の数は6通り。
そのうち,12以下になるのは,(1,3),(1,6),(1,10),(3,6)の4通りあるので,2/3
②3枚取り出したとき12以下となる場合が2通りしかない場合は次のように考える。
[1]まずxを使わない 1+3+6=10で一通りは必ずこれになる。
[2]xを使う 1+3+x=4+xが12以下でなくてはならず,
1+6+x=7+xは12より大きくなければならない。
これを考えると,x=8,7のみである。
[5]選択問題:学校によって採択が異なりますが,全て折り曲げの問題です。
[Ⅰ](1)①∠EDC=60°
②Dから垂線を下ろせば,△DECと同じ形の図形が現れることがわかる。よって△DCEの4倍である。
(2)BG=xとすると,AG=x,GC=6√3-xであるから,
△BGCで三平方の定理より,x^2=(6√3-x)^2+6^2 x=4√3
[Ⅱ](1)折り曲げた図形があるので,同じ角度の部分がたくさんできる。
四角形DGECは台形であるから,
∠DGE+∠GEC=180°。∠DGF=38°,∠FGE=90°であるから,∠GEC=52°
よって∠GEFはその半分であるから,26°
(2)JIB=60°,∠JIC=120°であるから,∠JIH=∠HIC=60°となる。
錯角から∠IJH=60°で△JIHは正三角形になる。JからBCに垂線を下ろすと,
JI=6√3であることがわかる。△JHKも30°の三角定規の形であるから,KH=3√3
(3)まず,△ANMはAN=AMの二等辺三角形である。
①∠ANM=∠CNM(折り曲げたから)
②∠CNM=∠NMA(平行線の錯角) であるので
∠ANM=∠NMAで二等辺三角形である。
この三角形の面積はAMを底辺として高さをCDとする。
AN=xとすると,NC=x,BN=12-xであるから,△ABNで三平方の定理より,
6^2+(12-x)^2=^x2 → 36+144-24x=0
よって△AMN=15/2×6÷2=45/2(cm2)
[Ⅲ](1)この図ではNCのちょうど2倍がECになっているので,△ENCが30°の三角定規の形になっている。
よって∠ECD=30°,∠ECF=15°であるから,△FECの内角の和を考えて,∠EFC=75°
(2)AB=9,AG=4から,
DG=JG=5。△AJGで
3:4:5の三角形となる。
また,図のように等しい角度
を○とすると,△JBKも△KIH
も3:4:5の三角形になる。
JB=6から,JK=6×5/4=15/2。
KI=9-15/2=3/2で,IH=HC=3/2×4/3=2。
求める四角形GJIHの面積は四角形GDCHと等しいので,
(5+2)×9÷2=63/2
(3)図のようにCQを結ぶと
CP=CB(正方形の1辺)
CQは共通
∠CBQ=∠CPQ=90°
であるから,斜辺と他の1角が
それぞれ等しいので
△CBQ≡△CPQとなる。
AL=3,LD=2とすると,LP=2。QB=xとすると,AQ=5-xで,PQ=xより,
△ALQで三平方の定理より,
(5-x)^2+3^2=(2+x)^2 → 25-10x+x^2+9=4+4x+x^2
x=15/7→ より,AQ=20/7 。よって,AQはQBの4/3倍
平成22年度・岩手県(数学)高校入試問題 [平成22年度(2010年)・数学]
平成22年度・岩手県(数学)高校入試問題のダウンロードはこちらから
http://nokai.jp/iwate/test_mondai.htm
■■まとめ■■
標準的な問題ですが,問題量が若干多めなので時間が足りなくなってしまう場合も
あるでしょう。
★つきは1つあります。
●[11]パズル的要素の濃い問題ですが,途中まででできることがなくなります。
そのときにもしもここが0だったら…,と仮定して実際に実験をやっていく,
これが難しいでしょう。時間切れになってしまった人も多いかと思います。
■■ポイント■■
[1]計算問題。間違えたくない問題。
(1)-4-5=-9
(2)分数の問題
(3)平方根の計算問題
(4)x^2-7x+12=0 → 因数分解して,
(x-3)(x-4)=0 → x=3,4
(5)4x+2y=9 → 2y=9-4x → y=(9-4x)/2
[2]図形の基本的知識が問われる問題。
(1)△ADE∽△ACBであり,AD:AE=AC:AB=2:3であるから,AB=3/2AC=9(cm)
(2)外角の和は360°になることを使う。∠xの外角をyとして,
80+75+70+y+60=360を解くとy=75であるから,∠x=105°
(3)求める体積V=3×3×π×5=45π(cm3)
[3]比例の関係を式で表す。
400枚印刷するのに5分かかり,x枚印刷するのにy分かかる。
400:5=x:y → 400y=5x → y=1/80*x
[4]組み合わせの考え方を使う。
(1)5つの班から2つの班を選ぶ選び方は,(5×4)/(2×1)=10通り
(2)1班が選ばれる確率は,(1)の全10通りに対して,
(1班,2班),(1班,3班),(1班,4班),(1班,5班)
の4通りがあるので, 4/10=2/5
[5]聞かれていることは角度に関すること。
(1)△ABCは60度の三角定規の形になっているので,AC=2cm。この段階で△ACDが二等辺
三角形であることに気づく。
(2)まず∠BADが90°だから,∠DAC=30°
△ACDが二等辺三角形だから∠ACD=75°
∠BCF=180-75-30=75°。…①
また,∠AEB=50°だから対頂角で∠CEF=50°…②
①・②より,△CEFの内角の和より,∠CFE=55°
[6]EPが通過した部分を3つの場合に関して図に表せばよい。
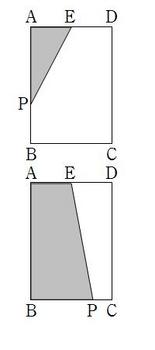
(1)AB上を動くときは,図のような状況であり,
三角形の面積となる。y=2×x÷2=x よってy=x
(2)BC上を動くときは,図のような状況であり,
台形の面積となる。
AB+BP=xだからBP=x-6となることに注意
して,
y=(2+x-6)/2*6÷2=3x/2 -2
(3)最後,CD上を動くときは,AB+BC+CP=x
だから,CP=x-10であるが,この場合は
四角形全体から△EDPを引いて面積を求める。
DP=CD-CP=6-(x-10)=16-xだから,
y=6×4-2*(16-x)÷2=8+x
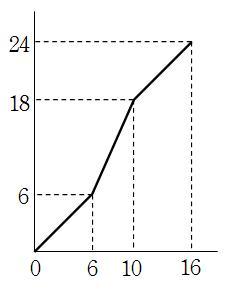
後は変域に注意してグラフ
を書くと,右のようになる。
[7]連立方程式の基本的な問題。
ノート1冊x円,ボールペン1本y円とすると,
x+y=450
0.8x+0.9y=390
ここでは,x=450-yとして,代入法を使うと,
0.8(450-y)+0.9y=390
360+0.1y=390 → y=300,x=150
よって,ノート1冊150円,ボールペン1本300円
[8]相似の証明なので「2角が等しい…かな?」と考えながら証明を完成させればよい。
(証明)△ABCと△DEBにおいて,
弧BCに対する円周角は等しいので,
∠BAC=∠EDB …①
弧ABに対する円周角は等しいので,
∠ADB=∠ACB …②
平行線の錯角は等しいので,
∠ADB=∠DBE …③
②・③より,∠ACB=∠DBE …④
①・④より,2角がそれぞれ等しいので,
△ABC∽△DEB (証明終)
[9]2次関数の問題。数字を元に,具体的にどんどん計算をして行こう。
(1)Aのy座標はx座標がわかっているので,y=2x^2に代入して,y=2×2^2=8
(2)Cはx座標が2なのでy座標はy=ax^2に代入して,
y=4aと表される。
△OAC=(8-4a)×2÷2=8-4a,△OBE=8×2÷2=8 より,
8-4a:8=2:3 → 16=24-12a → a=2/3 でy座標が8を代入すると,
x2=12 → x=±2√3 より,Dのx座標は -2√3
[10]展開図は慣れてないと難しいか。
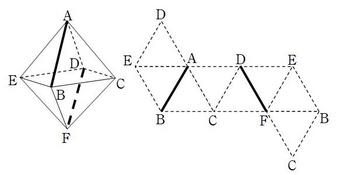
(1)図のように記号を振りながら行う。
(例)辺ABを持つ三角形は△ABCで…,今度は辺ACを持つ三角形は△ACDで…,と順番に
埋めていけば自然と埋まっていく。
(2)△正四角すいが2つ重なった形を考える。
△ABDを抜き出すとBD=2√2,(高さ)=√2であるから,(正四角すい)=2×2×√2×1/3=4√2/3
よって(正八面体)=8√2/3
[11]少しずつ丁寧にやっていこう。試験中では時間切れになってしまうのではなかろうか。
(1)5行目までは問題文に書いてあるので,
5行目 1 0 2 0 1
6行目 1 1 2 2 1 1
7行目 1 2 3 0 3 2 1
8行目 1 3 1 3 3 1 3 1 となる。
(2)これは,1つ1つ丁寧にやっていく。
0 [ア] [イ] [ウ] [エ] [オ] 0
0 [カ] [キ] [ク] [ケ] [コ] 2
3 [サ] [シ] [ス] [セ] [ソ] 0
3 [タ] 2 1 [チ] 0
よく見る。まず[オ]=2。[ソ]=0から,[コ]=2→[エ]=0
[カ]=3から,[ア]=3。[サ]=0から,[キ]=1→[イ]=2。
ここまで来ると,手詰まりになる。
そこで[ウ][ク][ケ][シ][ス][セ]の部分から下の2,1の部分までは,[ウ]=0のとき,1のとき,2のとき…などと順番にやっていくとうまくいかない。[ウ]=3のときぴったりうまくいくことがわかる。よって,
[ア][イ][ウ][エ][オ]=3 2 3 0 2
http://nokai.jp/iwate/test_mondai.htm
■■まとめ■■
標準的な問題ですが,問題量が若干多めなので時間が足りなくなってしまう場合も
あるでしょう。
★つきは1つあります。
●[11]パズル的要素の濃い問題ですが,途中まででできることがなくなります。
そのときにもしもここが0だったら…,と仮定して実際に実験をやっていく,
これが難しいでしょう。時間切れになってしまった人も多いかと思います。
■■ポイント■■
[1]計算問題。間違えたくない問題。
(1)-4-5=-9
(2)分数の問題
(3)平方根の計算問題
(4)x^2-7x+12=0 → 因数分解して,
(x-3)(x-4)=0 → x=3,4
(5)4x+2y=9 → 2y=9-4x → y=(9-4x)/2
[2]図形の基本的知識が問われる問題。
(1)△ADE∽△ACBであり,AD:AE=AC:AB=2:3であるから,AB=3/2AC=9(cm)
(2)外角の和は360°になることを使う。∠xの外角をyとして,
80+75+70+y+60=360を解くとy=75であるから,∠x=105°
(3)求める体積V=3×3×π×5=45π(cm3)
[3]比例の関係を式で表す。
400枚印刷するのに5分かかり,x枚印刷するのにy分かかる。
400:5=x:y → 400y=5x → y=1/80*x
[4]組み合わせの考え方を使う。
(1)5つの班から2つの班を選ぶ選び方は,(5×4)/(2×1)=10通り
(2)1班が選ばれる確率は,(1)の全10通りに対して,
(1班,2班),(1班,3班),(1班,4班),(1班,5班)
の4通りがあるので, 4/10=2/5
[5]聞かれていることは角度に関すること。
(1)△ABCは60度の三角定規の形になっているので,AC=2cm。この段階で△ACDが二等辺
三角形であることに気づく。
(2)まず∠BADが90°だから,∠DAC=30°
△ACDが二等辺三角形だから∠ACD=75°
∠BCF=180-75-30=75°。…①
また,∠AEB=50°だから対頂角で∠CEF=50°…②
①・②より,△CEFの内角の和より,∠CFE=55°
[6]EPが通過した部分を3つの場合に関して図に表せばよい。
(1)AB上を動くときは,図のような状況であり,
三角形の面積となる。y=2×x÷2=x よってy=x
(2)BC上を動くときは,図のような状況であり,
台形の面積となる。
AB+BP=xだからBP=x-6となることに注意
して,
y=(2+x-6)/2*6÷2=3x/2 -2
(3)最後,CD上を動くときは,AB+BC+CP=x
だから,CP=x-10であるが,この場合は
四角形全体から△EDPを引いて面積を求める。
DP=CD-CP=6-(x-10)=16-xだから,
y=6×4-2*(16-x)÷2=8+x
後は変域に注意してグラフ
を書くと,右のようになる。
[7]連立方程式の基本的な問題。
ノート1冊x円,ボールペン1本y円とすると,
x+y=450
0.8x+0.9y=390
ここでは,x=450-yとして,代入法を使うと,
0.8(450-y)+0.9y=390
360+0.1y=390 → y=300,x=150
よって,ノート1冊150円,ボールペン1本300円
[8]相似の証明なので「2角が等しい…かな?」と考えながら証明を完成させればよい。
(証明)△ABCと△DEBにおいて,
弧BCに対する円周角は等しいので,
∠BAC=∠EDB …①
弧ABに対する円周角は等しいので,
∠ADB=∠ACB …②
平行線の錯角は等しいので,
∠ADB=∠DBE …③
②・③より,∠ACB=∠DBE …④
①・④より,2角がそれぞれ等しいので,
△ABC∽△DEB (証明終)
[9]2次関数の問題。数字を元に,具体的にどんどん計算をして行こう。
(1)Aのy座標はx座標がわかっているので,y=2x^2に代入して,y=2×2^2=8
(2)Cはx座標が2なのでy座標はy=ax^2に代入して,
y=4aと表される。
△OAC=(8-4a)×2÷2=8-4a,△OBE=8×2÷2=8 より,
8-4a:8=2:3 → 16=24-12a → a=2/3 でy座標が8を代入すると,
x2=12 → x=±2√3 より,Dのx座標は -2√3
[10]展開図は慣れてないと難しいか。
(1)図のように記号を振りながら行う。
(例)辺ABを持つ三角形は△ABCで…,今度は辺ACを持つ三角形は△ACDで…,と順番に
埋めていけば自然と埋まっていく。
(2)△正四角すいが2つ重なった形を考える。
△ABDを抜き出すとBD=2√2,(高さ)=√2であるから,(正四角すい)=2×2×√2×1/3=4√2/3
よって(正八面体)=8√2/3
[11]少しずつ丁寧にやっていこう。試験中では時間切れになってしまうのではなかろうか。
(1)5行目までは問題文に書いてあるので,
5行目 1 0 2 0 1
6行目 1 1 2 2 1 1
7行目 1 2 3 0 3 2 1
8行目 1 3 1 3 3 1 3 1 となる。
(2)これは,1つ1つ丁寧にやっていく。
0 [ア] [イ] [ウ] [エ] [オ] 0
0 [カ] [キ] [ク] [ケ] [コ] 2
3 [サ] [シ] [ス] [セ] [ソ] 0
3 [タ] 2 1 [チ] 0
よく見る。まず[オ]=2。[ソ]=0から,[コ]=2→[エ]=0
[カ]=3から,[ア]=3。[サ]=0から,[キ]=1→[イ]=2。
ここまで来ると,手詰まりになる。
そこで[ウ][ク][ケ][シ][ス][セ]の部分から下の2,1の部分までは,[ウ]=0のとき,1のとき,2のとき…などと順番にやっていくとうまくいかない。[ウ]=3のときぴったりうまくいくことがわかる。よって,
[ア][イ][ウ][エ][オ]=3 2 3 0 2
平成22年度・神奈川県(数学)高校入試問題 [平成22年度(2010年)・数学]
平成22年度・神奈川県(数学)高校入試問題のダウンロードはこちらから
http://www.tokyo-np.co.jp/k-shiken/index.html
■■ 「弧に円周角を書く」手法のビデオはこちら ■■
[7](イ)では「弧に円周角を書く」という手法をしっかり勉強してください。
参考ビデオがありますので,こちらもあわせてみておいてください。
「弧に円周角を書く」手法のビデオを見る。
■■まとめ■■
標準的な問題です。前から順番に解いていけば問題ありません。
解ける問題から考えていきましょう。
★★つきは3つ。
[3](ウ)関数の面積で,具体的に面積を出さなくてもよい方法を覚えておきましょう。
[6](イ)Kの位置をしっかりと捉えましょう。
[7](イ)角度の出し方は補助線をめいいっぱい引くのではなく,弧に円周角を書く,
という方式で行うこと。
■■ポイント■■
[1]計算問題。ここは取り立ててやる問題はない。
(ア)-5+(-8)=-13
(イ)2-6×(3-5)=2-6×(-2)=14
(ウ)分数の計算。
(エ)14a2b÷2b =7a2
(オ)通分してから計算する。
(カ)有理化してから計算する。
(キ)(x+2)^2-(x+3)(x-4)=x^2+4x+4-(x^2-x-12)=5x+16
[2]小問集合。計算が多い。
(ア)(x-1)(x-4)-10=x^2-5x-6=(x-6)(x+1)
(イ)(x+5)^2=7 → x+5=±√7 → x=-5±√7
(ウ) ①×3-②×2をすると,9y+10y=3-22 これより,y=-1。①に代入して,
2x-3=1 → 2x=4 → x=2。(x,y)=(2,-1)
(エ)関数y=ax2でxがpからqまで変化するときの変化の割合は,a(p+q)である。
よって(変)=-1/2×(2+4) -3
(オ)HI=EF-(EH+IF)という考え方で考える。
AE:ED=1:3→EH=3/4 。(△AEH∽△ADC)
BF:FC=1:3→IF=1/2 。(△BIF∽△BCG)
これより,引き算して,HI=7/4(cm)
[3]2次関数の問題。(3)は比を求めればよいことに気づきたい問題。
(1)直線①上に点Aがあるから,y=x+6に代入すると,A(6,9)。これをy=ax^2に代入すると,
9=36a → a=1/4
(2)Bの座標は直線①がx軸と交わるところでB(-3,0)。Dの座標はAのy座標が9だからD(0,9)
よって直線BDは傾き3,切片9でy=3x+9
(3)具体的に面積を求めなくてよい問題である。
△AEF:△ADFはEF:DFの線分比に等しいが,△ADF∽△BEFだから,
EF:DF=BE:AD=9:6=3:2。よって,DF:FE=2:3から,△AEF:△ADE=3:5
△ADEと△BCDは底辺の長さも高さも等しいので,△AEF:△BCD=3:5
[4]袋からカードを出して,指定された玉を取り除く。設定をしっかりと理解したい。
全体の場合の数は5×5の25通りである。
(ア)まずはAかBのカードを取る。そして,袋Yからは,1のカードを取ればよい。よって, 2/25
(イ)もともと全部で30個(→3の倍数)入っているので,残っている数が3の倍数ならば,取り除く数
も3の倍数である。袋Xからそれぞれのカードを取ったときどうなるかを考える。
A→5箱から取り除くので,袋Yは3のみよい。
B→4箱から取り除くので,袋Yは3のみよい。
C→3箱から取り除くので,袋Yはどれでもよい。
C→2箱から取り除くので,袋Yは3のみよい。
C→4箱から取り除くので,袋Yは3のみよい。
よって全部で9通りあるので, 9/25
[5]n=3や4の場合について考えて,それを一般化していく。例えば,n=3のときは,
①線分p上に2本,線分q上に2本。
②線分pの3点から線分qの3点に向かって,3×3=9本。
この合計で2+2+9=13本。
(ア)上と同じ考え方をすると,n=4のとき,
①線分p上に3本,線分q上に3本。
②線分pの4点から線分qの4点に向かって,4×4=16本。
この合計で3+3+16=22本。
(イ)一般化すると,
①線分p上に(n-1)本,線分q上に(n-1)本。
②線分pのn個の点から線分qのn個の点に向かって,n×n=n^2本。
合計すると,n^2+2(n-1)=253
n^2+2n-255=0 → (n+17)(n-15)=0。nはもちろん正の数なので,n=15
[6]立体図形の考え方の問題。
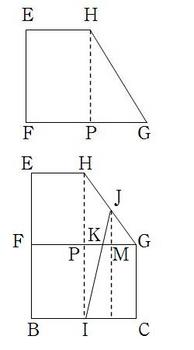
(ア)底面積(2つ分)は(3+6)×4÷2×2=36。
側面積は(EF+FG+GH+HEの長さ)×AE
で一気に求める。図のようにHからFGに
垂線HPを下ろすと,FP=PG=3,EF=4か
ら三平方の定理よりHG=5。
よって,側面積は (4+6+5+3)×4=72。
だから合計して,36+72=108。
(イ)まずは,Kがどこかを明らかにしない
といけない。図のように,展開図のHや
Jから垂線を下ろしそれぞれ名前をつけ
る。JはHGの中点だから,MはPGの中点。
さらにJMはHPの半分の長さである。
よって,
△PIK∽△MJKで相似比は2:1。→PK:KM=2:1
PM=1.5cmだから,PK=1cm→FK=4cmである。
よって,AKの長さは直方体の対角線の公式を使って,
AK=√(4^2+4^2+4^2)=4√3(cm)
[7]証明と角度に関する問題。図がちょっと複雑であるので,注意したい。
(ア)証明の穴埋め問題。答えがすぐそばに書いてある。
①∠AEC=∠ADCとなるのは弧ACに対する円周角が等しいから。
②∠ADC=∠GCDとなるのは平行線の錯角。
③OA=ODの二等辺三角形だから∠OAD=∠ODA
④∠ODA=∠OGCとなるのは平行線の同位角。
⑤最後の相似条件は角度に関することで証明をしているので,2角がそれぞれ等しい。
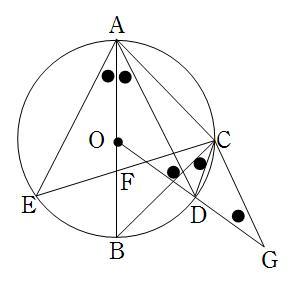
(イ)等しい角度に印をつけた。
①∠BCD=∠BAD(弧BDに対する円周角)
②∠BAD=∠BAE(仮定)
③∠FAE=∠DGC(アの証明より)
④∠OAD=∠ODA(二等辺三角形)
つまり●は全て26°である。
求める∠AFEはアルハゼンの定理が使える形であり,
(弧AEに対する円周角)+(弧BCに対する円周角)
弧AE=90-26=64°分
弧BC=41°分であるから, 合計して105°
※アルハゼンの定理は,「弧の上に円周角を書き込む」という手法を使ったときに出てくる定理で,
覚えておくと便利なものです。
http://www.tokyo-np.co.jp/k-shiken/index.html
■■ 「弧に円周角を書く」手法のビデオはこちら ■■
[7](イ)では「弧に円周角を書く」という手法をしっかり勉強してください。
参考ビデオがありますので,こちらもあわせてみておいてください。
「弧に円周角を書く」手法のビデオを見る。
■■まとめ■■
標準的な問題です。前から順番に解いていけば問題ありません。
解ける問題から考えていきましょう。
★★つきは3つ。
[3](ウ)関数の面積で,具体的に面積を出さなくてもよい方法を覚えておきましょう。
[6](イ)Kの位置をしっかりと捉えましょう。
[7](イ)角度の出し方は補助線をめいいっぱい引くのではなく,弧に円周角を書く,
という方式で行うこと。
■■ポイント■■
[1]計算問題。ここは取り立ててやる問題はない。
(ア)-5+(-8)=-13
(イ)2-6×(3-5)=2-6×(-2)=14
(ウ)分数の計算。
(エ)14a2b÷2b =7a2
(オ)通分してから計算する。
(カ)有理化してから計算する。
(キ)(x+2)^2-(x+3)(x-4)=x^2+4x+4-(x^2-x-12)=5x+16
[2]小問集合。計算が多い。
(ア)(x-1)(x-4)-10=x^2-5x-6=(x-6)(x+1)
(イ)(x+5)^2=7 → x+5=±√7 → x=-5±√7
(ウ) ①×3-②×2をすると,9y+10y=3-22 これより,y=-1。①に代入して,
2x-3=1 → 2x=4 → x=2。(x,y)=(2,-1)
(エ)関数y=ax2でxがpからqまで変化するときの変化の割合は,a(p+q)である。
よって(変)=-1/2×(2+4) -3
(オ)HI=EF-(EH+IF)という考え方で考える。
AE:ED=1:3→EH=3/4 。(△AEH∽△ADC)
BF:FC=1:3→IF=1/2 。(△BIF∽△BCG)
これより,引き算して,HI=7/4(cm)
[3]2次関数の問題。(3)は比を求めればよいことに気づきたい問題。
(1)直線①上に点Aがあるから,y=x+6に代入すると,A(6,9)。これをy=ax^2に代入すると,
9=36a → a=1/4
(2)Bの座標は直線①がx軸と交わるところでB(-3,0)。Dの座標はAのy座標が9だからD(0,9)
よって直線BDは傾き3,切片9でy=3x+9
(3)具体的に面積を求めなくてよい問題である。
△AEF:△ADFはEF:DFの線分比に等しいが,△ADF∽△BEFだから,
EF:DF=BE:AD=9:6=3:2。よって,DF:FE=2:3から,△AEF:△ADE=3:5
△ADEと△BCDは底辺の長さも高さも等しいので,△AEF:△BCD=3:5
[4]袋からカードを出して,指定された玉を取り除く。設定をしっかりと理解したい。
全体の場合の数は5×5の25通りである。
(ア)まずはAかBのカードを取る。そして,袋Yからは,1のカードを取ればよい。よって, 2/25
(イ)もともと全部で30個(→3の倍数)入っているので,残っている数が3の倍数ならば,取り除く数
も3の倍数である。袋Xからそれぞれのカードを取ったときどうなるかを考える。
A→5箱から取り除くので,袋Yは3のみよい。
B→4箱から取り除くので,袋Yは3のみよい。
C→3箱から取り除くので,袋Yはどれでもよい。
C→2箱から取り除くので,袋Yは3のみよい。
C→4箱から取り除くので,袋Yは3のみよい。
よって全部で9通りあるので, 9/25
[5]n=3や4の場合について考えて,それを一般化していく。例えば,n=3のときは,
①線分p上に2本,線分q上に2本。
②線分pの3点から線分qの3点に向かって,3×3=9本。
この合計で2+2+9=13本。
(ア)上と同じ考え方をすると,n=4のとき,
①線分p上に3本,線分q上に3本。
②線分pの4点から線分qの4点に向かって,4×4=16本。
この合計で3+3+16=22本。
(イ)一般化すると,
①線分p上に(n-1)本,線分q上に(n-1)本。
②線分pのn個の点から線分qのn個の点に向かって,n×n=n^2本。
合計すると,n^2+2(n-1)=253
n^2+2n-255=0 → (n+17)(n-15)=0。nはもちろん正の数なので,n=15
[6]立体図形の考え方の問題。
(ア)底面積(2つ分)は(3+6)×4÷2×2=36。
側面積は(EF+FG+GH+HEの長さ)×AE
で一気に求める。図のようにHからFGに
垂線HPを下ろすと,FP=PG=3,EF=4か
ら三平方の定理よりHG=5。
よって,側面積は (4+6+5+3)×4=72。
だから合計して,36+72=108。
(イ)まずは,Kがどこかを明らかにしない
といけない。図のように,展開図のHや
Jから垂線を下ろしそれぞれ名前をつけ
る。JはHGの中点だから,MはPGの中点。
さらにJMはHPの半分の長さである。
よって,
△PIK∽△MJKで相似比は2:1。→PK:KM=2:1
PM=1.5cmだから,PK=1cm→FK=4cmである。
よって,AKの長さは直方体の対角線の公式を使って,
AK=√(4^2+4^2+4^2)=4√3(cm)
[7]証明と角度に関する問題。図がちょっと複雑であるので,注意したい。
(ア)証明の穴埋め問題。答えがすぐそばに書いてある。
①∠AEC=∠ADCとなるのは弧ACに対する円周角が等しいから。
②∠ADC=∠GCDとなるのは平行線の錯角。
③OA=ODの二等辺三角形だから∠OAD=∠ODA
④∠ODA=∠OGCとなるのは平行線の同位角。
⑤最後の相似条件は角度に関することで証明をしているので,2角がそれぞれ等しい。
(イ)等しい角度に印をつけた。
①∠BCD=∠BAD(弧BDに対する円周角)
②∠BAD=∠BAE(仮定)
③∠FAE=∠DGC(アの証明より)
④∠OAD=∠ODA(二等辺三角形)
つまり●は全て26°である。
求める∠AFEはアルハゼンの定理が使える形であり,
(弧AEに対する円周角)+(弧BCに対する円周角)
弧AE=90-26=64°分
弧BC=41°分であるから, 合計して105°
※アルハゼンの定理は,「弧の上に円周角を書き込む」という手法を使ったときに出てくる定理で,
覚えておくと便利なものです。
平成22年度・東京都(数学)高校入試問題 [平成22年度(2010年)・数学]
平成22年度・東京都(数学)高校入試問題のダウンロードはこちらから
http://www.tokyo-np.co.jp/k-shiken/index.html
■■まとめ■■
標準的な問題です。問題の難易がはっきりしています。
解ける問題から考えていきましょう。
★★つきは3つ。
●[3](3)関数の面積の求め方。たて×横の考え方を使えるか。
●[4](2)②比あわせの考え方を経験したことがあるか。
●[5](2)実は[3](3)と考え方は同じ。立体になっているだけの問題。
■■ポイント■■
[1]小問集合。
(1)正負の計算。問題ない。
(2)1次式の文字式の計算。これも問題ない。
(3)平方根の計算。乗法公式を使う。
(4)1次方程式を解く。問題ない。
(5)下式をx=7-5yとして代入法でも,加減法でもよい。
(6)(x+2)2=36 → x+2=±6 → x=-2±6 = 4,-8
(7)bがaの倍数となる場合,aから考えると,
1の倍数→b=1~6 2の倍数→b=2,4,6 3の倍数→b=3,6。
4の倍数→b=4 5の倍数→b=5。 6の倍数→b=6 合計14通り。
(8)△AEOの外角で考える。
①∠DABは半円の弧の円周角の で15°
②∠AOCは120°であるから,合計135°
(9)AP=BPのとき,点Pは線分ABの垂直二等分線の上にある。
この作図をすればよい。
[2]面を動かすと立体になる,という考え方の問題。
(1)P=a^2 hである。面積と高さを掛ければよい。
(2)体積を求める式を作ればよい。
この立体を底面積×高さ,という式を使って求めると,
AD=aであるから,
V=a×a×π×a=πa^3となる。…①
ここで,lを求めると,lは直径aの円周の長さに等しいので,l=πa…②
②を①に代入すると,V=a^2lとなる。
[3]関数であるが1次関数のみ。面積の求め方は頻出のパターンなので覚えておく。
(1)点Pが直線l上にあるので,座標を代入する。
(2)mの傾きが のとき直線mの式は よって,これを直線lと連立させる。
★★(3)関数で面積を求める方法は,次のような方法を使うことを覚えよう。
△ARQの面積をPRで2つに分ける。すると,△APRと△PRQの和となる。
この2つの三角形の高さの和は14であるから,PR×14÷2=49。
これを解くと,PR=7(cm)となる。
[4]平面図形の相似の問題。最後の比あわせを今まで経験したことがあるかどうか。
(1)∠BAP=a°。∠BPA=a°よって,∠ABP=180-2a
である。よって,∠PBC=90-(180-2a)=2a-90(度)
(2)①証明は簡単にこなしたいところ。
△ABQと△CPQで
AB//CP(長方形の性質)であるから
∠ABQ=∠CPQ(平行線の錯角)…①
また∠AQB=∠CQP(対頂角)…②
①・②より2角がそれぞれ等しいので,△ABQ∽△CPQ
②CRの延長とABの交点をSとする。
AP//CSであるから,四角形ASCPは平行四辺形になり,AS:SB=2:1
△SBR∽△CPRからBR:RP=1:2=5:10
△ABQ∽△CPQから,BQ:QP=3:2=9:6となる。
よって,BR:RQ:QP=5:4:6となる。(比あわせをした)
以上より,QRはBPの 4/15倍である。
[5]立体の見方。(2)は経験がないと難しいだろう。
(1)△PFHは正三角形になることは問題ないだろう。60°
(2)先ほどの関数で面積を求めた問題に考え方は似ている。この立体を面DBFHで切ったときの
面を底面として,体積を求めればよいのである。
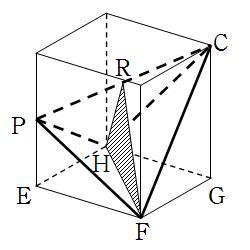
つまり,△RHFを底面として,左側の三角すい
と右側の三角すいの和と考えるが,その三角す
いの高さの和は6√2である。△PHFの高さは,
EPとCGの平均で,4.5
△PHFの面積は6√2×4.5×1/2
この立体の高さは6√2であるから,
6√2×4.5×1/2×6√2×1/3= 54(cm3)
※最後にこれはすい体なので1/3していることに注意!!
http://www.tokyo-np.co.jp/k-shiken/index.html
■■まとめ■■
標準的な問題です。問題の難易がはっきりしています。
解ける問題から考えていきましょう。
★★つきは3つ。
●[3](3)関数の面積の求め方。たて×横の考え方を使えるか。
●[4](2)②比あわせの考え方を経験したことがあるか。
●[5](2)実は[3](3)と考え方は同じ。立体になっているだけの問題。
■■ポイント■■
[1]小問集合。
(1)正負の計算。問題ない。
(2)1次式の文字式の計算。これも問題ない。
(3)平方根の計算。乗法公式を使う。
(4)1次方程式を解く。問題ない。
(5)下式をx=7-5yとして代入法でも,加減法でもよい。
(6)(x+2)2=36 → x+2=±6 → x=-2±6 = 4,-8
(7)bがaの倍数となる場合,aから考えると,
1の倍数→b=1~6 2の倍数→b=2,4,6 3の倍数→b=3,6。
4の倍数→b=4 5の倍数→b=5。 6の倍数→b=6 合計14通り。
(8)△AEOの外角で考える。
①∠DABは半円の弧の円周角の で15°
②∠AOCは120°であるから,合計135°
(9)AP=BPのとき,点Pは線分ABの垂直二等分線の上にある。
この作図をすればよい。
[2]面を動かすと立体になる,という考え方の問題。
(1)P=a^2 hである。面積と高さを掛ければよい。
(2)体積を求める式を作ればよい。
この立体を底面積×高さ,という式を使って求めると,
AD=aであるから,
V=a×a×π×a=πa^3となる。…①
ここで,lを求めると,lは直径aの円周の長さに等しいので,l=πa…②
②を①に代入すると,V=a^2lとなる。
[3]関数であるが1次関数のみ。面積の求め方は頻出のパターンなので覚えておく。
(1)点Pが直線l上にあるので,座標を代入する。
(2)mの傾きが のとき直線mの式は よって,これを直線lと連立させる。
★★(3)関数で面積を求める方法は,次のような方法を使うことを覚えよう。
△ARQの面積をPRで2つに分ける。すると,△APRと△PRQの和となる。
この2つの三角形の高さの和は14であるから,PR×14÷2=49。
これを解くと,PR=7(cm)となる。
[4]平面図形の相似の問題。最後の比あわせを今まで経験したことがあるかどうか。
(1)∠BAP=a°。∠BPA=a°よって,∠ABP=180-2a
である。よって,∠PBC=90-(180-2a)=2a-90(度)
(2)①証明は簡単にこなしたいところ。
△ABQと△CPQで
AB//CP(長方形の性質)であるから
∠ABQ=∠CPQ(平行線の錯角)…①
また∠AQB=∠CQP(対頂角)…②
①・②より2角がそれぞれ等しいので,△ABQ∽△CPQ
②CRの延長とABの交点をSとする。
AP//CSであるから,四角形ASCPは平行四辺形になり,AS:SB=2:1
△SBR∽△CPRからBR:RP=1:2=5:10
△ABQ∽△CPQから,BQ:QP=3:2=9:6となる。
よって,BR:RQ:QP=5:4:6となる。(比あわせをした)
以上より,QRはBPの 4/15倍である。
[5]立体の見方。(2)は経験がないと難しいだろう。
(1)△PFHは正三角形になることは問題ないだろう。60°
(2)先ほどの関数で面積を求めた問題に考え方は似ている。この立体を面DBFHで切ったときの
面を底面として,体積を求めればよいのである。
つまり,△RHFを底面として,左側の三角すい
と右側の三角すいの和と考えるが,その三角す
いの高さの和は6√2である。△PHFの高さは,
EPとCGの平均で,4.5
△PHFの面積は6√2×4.5×1/2
この立体の高さは6√2であるから,
6√2×4.5×1/2×6√2×1/3= 54(cm3)
※最後にこれはすい体なので1/3していることに注意!!
平成22年度・青森県(数学)高校入試問題 [平成22年度(2010年)・数学]
平成22年度・青森県(数学)高校入試問題のダウンロードはこちらから
http://www.pref.aomori.lg.jp/bunka/education/H22zenki-ac.html
■■まとめ■■
簡単な問題から難しい問題へと少しずつ難しくなっていっている問題です。
[5]の問題は,2つの立体の置く方向を変えても問題ないこと。
計算が煩雑になりやすい部分を,どう処理するか。
という点を考えるとよいでしょう。
■■ポイント■■
[1]計算問題と小問集合。さっと片付けたい。
(1)ア~エ.基本的な問題
オ.平方根の問題。有理化しながら行う。
(2)式変形すると,8xy^2となるから,ここで代入する。8×3×(-1)2=24
(3)x^2-5x=24 → x^2-5x-24=0 → (x-8)(x+3)=0 → x=8,-3
(4)x,yを代入して,a,bの連立方程式として求める。
(5)Aの座標は(-2,-3)であるから,原点対称である点は,A'(2,3)
(6)円Oの半径をrとすると,底面の周の長さと,側面の周の長さが等しいので,
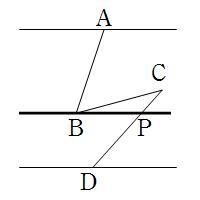
(7)尖っている部分に線を入れる。
錯角で∠ABP=75°,錯角で∠BPD=40°
△BPCの外角で,∠CBP=15°
よって,∠x=∠ABC=60°
(8)ABの中点をHとして,△AOHで三平方の定理を使う。円Oの半径が7であるから,
AH=√49-16=√33。よってAB=2AH=2√33
[2]ここも小問集合。
(1)できるカードは6通りだけ。12,13,21,23,31,32。
この中で素数は13,23,31であるから, 1/2
(2)平方根の中が平方数になっていればよい。
n=2,2×2^2,2×3^2,2×2^2×3^2=2,8,18,72
(3)一番小さい数をnとする。
(一番小さい数)×(一番大きい数)+1=n(n+2)+1となるが,式変形すると,
n(n+2)+1=n^2+2n+1=(n+1)^2
となる。これは真ん中の数の2乗であることを表しているので,予想はいつでも成立する。
[3]図形に関する問題。図はあまり難しくない。
(1)[ア]AB=BC
[イ]∠ABD=∠BCE=60°
[ウ]∠BAD=∠CBE
[エ]よって,1辺とその両端の角が等しいので合同。
(2)正四角すいなので,底面は正方形である。
ア.正方形の対角線なので 6(cm)
イ.OA=5,AH=3であるから,3:4:5の三角形があるからOH=4。CからOAの距離は△OACの
面積を2通りで表せばよい。
[1]底辺AC,高さOH→6×4÷2
[2]底辺OA,高さCP→5×CP÷2。よってCP=24/5(cm)
[4]2次関数と直線の問題。ここは簡単である。
(1)ここはBを放物線の式に代入して終わりで,y=ax^2 → 2=4a → a=1/2
(2)Aのx座標は4→(1)よりy座標は8。B(-2,2),A(4,8)から,傾き1。y=x+4
(3)直線ABの切片は4であるから,4×6÷2=12
(4)斜めの長さの比は,x座標,y座標の比を考える。
AB間はx座標もy座標も6の差があるので,BC間はその1/4である3/2だけBよりも小さい。
よって,C(-7/2,1/2)である。これをy=bx2に代入すると,b=2/49
[5]水槽に水を入れていく問題で,すこしずつ丁寧に見ていく必要がある。グラフに必要なことを書き
ながら行っていこう。
(1)ア.グラフの傾きが変化するところは80秒後。つまり,最初の80秒間は底面積が小さいところの
話である。毎秒60cm3を80秒入れると4800(cm3)水が入り,
15×20=300(cm2)が最初の底面積だから,AB=16(cm)
イ.224-80=144(秒)を入れたから,144×60=8640(cm3)の水を入れた。
高さは34-16=18(cm)であるから,15×CD×18=8640。これより,CD=32(cm)
(2)ア.底面積がしだいに大きくなっていくので,傾きが少しずつ小さくなっていく。
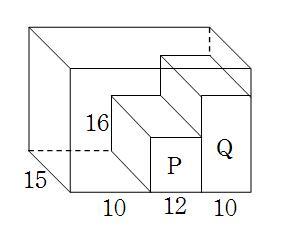
イ.少しずつ考える。ちなみに
Qを横においても縦におい
ても状況は変わらないので,
縦に置く。(15cmなのですっ
ぽり埋まる。)。
Qの高さをxとする。
A.最初の表面積は15×10(cm2)であり,16cm分水を入れる。
B.PとQの差の部分の表面積は22×15(cm2)であり,x-16(cm)分水を入れる。
C.最後の表面積は32×15(cm2)であり,5(cm)分だけ水を入れる。まとめると,
15×10×16+15×22(x-16)+15×32×5=75×86。
(いきなり計算しないで約分する!!) まず15で。
10×16+22(x-16)+32×5=5×86。 次2で。
10×8+11(x-16)+16×5=5×43。ここで計算。
80+11x-176+80=215
11x=231 → x=21(cm)。
http://www.pref.aomori.lg.jp/bunka/education/H22zenki-ac.html
■■まとめ■■
簡単な問題から難しい問題へと少しずつ難しくなっていっている問題です。
[5]の問題は,2つの立体の置く方向を変えても問題ないこと。
計算が煩雑になりやすい部分を,どう処理するか。
という点を考えるとよいでしょう。
■■ポイント■■
[1]計算問題と小問集合。さっと片付けたい。
(1)ア~エ.基本的な問題
オ.平方根の問題。有理化しながら行う。
(2)式変形すると,8xy^2となるから,ここで代入する。8×3×(-1)2=24
(3)x^2-5x=24 → x^2-5x-24=0 → (x-8)(x+3)=0 → x=8,-3
(4)x,yを代入して,a,bの連立方程式として求める。
(5)Aの座標は(-2,-3)であるから,原点対称である点は,A'(2,3)
(6)円Oの半径をrとすると,底面の周の長さと,側面の周の長さが等しいので,
(7)尖っている部分に線を入れる。
錯角で∠ABP=75°,錯角で∠BPD=40°
△BPCの外角で,∠CBP=15°
よって,∠x=∠ABC=60°
(8)ABの中点をHとして,△AOHで三平方の定理を使う。円Oの半径が7であるから,
AH=√49-16=√33。よってAB=2AH=2√33
[2]ここも小問集合。
(1)できるカードは6通りだけ。12,13,21,23,31,32。
この中で素数は13,23,31であるから, 1/2
(2)平方根の中が平方数になっていればよい。
n=2,2×2^2,2×3^2,2×2^2×3^2=2,8,18,72
(3)一番小さい数をnとする。
(一番小さい数)×(一番大きい数)+1=n(n+2)+1となるが,式変形すると,
n(n+2)+1=n^2+2n+1=(n+1)^2
となる。これは真ん中の数の2乗であることを表しているので,予想はいつでも成立する。
[3]図形に関する問題。図はあまり難しくない。
(1)[ア]AB=BC
[イ]∠ABD=∠BCE=60°
[ウ]∠BAD=∠CBE
[エ]よって,1辺とその両端の角が等しいので合同。
(2)正四角すいなので,底面は正方形である。
ア.正方形の対角線なので 6(cm)
イ.OA=5,AH=3であるから,3:4:5の三角形があるからOH=4。CからOAの距離は△OACの
面積を2通りで表せばよい。
[1]底辺AC,高さOH→6×4÷2
[2]底辺OA,高さCP→5×CP÷2。よってCP=24/5(cm)
[4]2次関数と直線の問題。ここは簡単である。
(1)ここはBを放物線の式に代入して終わりで,y=ax^2 → 2=4a → a=1/2
(2)Aのx座標は4→(1)よりy座標は8。B(-2,2),A(4,8)から,傾き1。y=x+4
(3)直線ABの切片は4であるから,4×6÷2=12
(4)斜めの長さの比は,x座標,y座標の比を考える。
AB間はx座標もy座標も6の差があるので,BC間はその1/4である3/2だけBよりも小さい。
よって,C(-7/2,1/2)である。これをy=bx2に代入すると,b=2/49
[5]水槽に水を入れていく問題で,すこしずつ丁寧に見ていく必要がある。グラフに必要なことを書き
ながら行っていこう。
(1)ア.グラフの傾きが変化するところは80秒後。つまり,最初の80秒間は底面積が小さいところの
話である。毎秒60cm3を80秒入れると4800(cm3)水が入り,
15×20=300(cm2)が最初の底面積だから,AB=16(cm)
イ.224-80=144(秒)を入れたから,144×60=8640(cm3)の水を入れた。
高さは34-16=18(cm)であるから,15×CD×18=8640。これより,CD=32(cm)
(2)ア.底面積がしだいに大きくなっていくので,傾きが少しずつ小さくなっていく。
イ.少しずつ考える。ちなみに
Qを横においても縦におい
ても状況は変わらないので,
縦に置く。(15cmなのですっ
ぽり埋まる。)。
Qの高さをxとする。
A.最初の表面積は15×10(cm2)であり,16cm分水を入れる。
B.PとQの差の部分の表面積は22×15(cm2)であり,x-16(cm)分水を入れる。
C.最後の表面積は32×15(cm2)であり,5(cm)分だけ水を入れる。まとめると,
15×10×16+15×22(x-16)+15×32×5=75×86。
(いきなり計算しないで約分する!!) まず15で。
10×16+22(x-16)+32×5=5×86。 次2で。
10×8+11(x-16)+16×5=5×43。ここで計算。
80+11x-176+80=215
11x=231 → x=21(cm)。
平成22年度・北海道・学校裁量(数学)高校入試問題 [平成22年度(2010年)・数学]
平成22年度・北海道・学校裁量(数学)高校入試問題のダウンロードはこちらから
http://www.koukou.hokkaido-c.ed.jp/gakuryokukensa/gakuryoku.html
■■まとめ■■
最後の[6]が学校裁量の問題です。(3)は今まで,類題を経験したかどうかがカギになります。
■■ポイント■■
[1]→共通問題[2]と同じ。
[2]→共通問題[3]と同じ。
[3]→共通問題[4]と同じ。
[4]→共通問題[5]と同じ。
[5]→共通問題[6]と同じ。
[6]ここが応用問題になっている。
問1 式を作って因数分解して考える問題である。三平方の定理より,
a^2=b^2=(2√15)^2 であるからこれを式変形すると,
a^2-b^2=60 → (a+b)(a-b)=60。 つまり掛け算して60。
あとは,これをシラミツブシに探していく。
①a+b=60,a-b=1のとき, →2a=61でaが自然数にならない。
②a+b=30,a-b=2のとき,これを解くと,(a,b)=(16,14)
③a+b=20,a-b=3のとき, →2a=23でaが自然数にならない。
④a+b=15,a-b=4のとき, →2a=19でaが自然数にならない。
⑤a+b=12,a-b=5のとき, →2a=17でaが自然数にならない。
⑥a+b=10,a-b=6のとき,これを解くと,(a,b)=(8,2)
問2 とりあえず全部で24通りしかないので,丁寧にやっていけば答えにたどり着く。
長さが√5になる,ということは,x座標・y座標の差が1と2のときだけである。
P=1のとき,(1,3),(b,1)であるから,Q=0,2 (y座標の差が2だから,x座標の差が1を探す)
P=2のとき,(2,3),(b,2)であるから,Q=0,4 (y座標の差が1だから,x座標の差が2を探す)
P=3のとき,(3,3),(b,3)で,このときは該当なし。
P=4のとき,(4,3),(b,4)であるから,Q=2,6 (y座標の差が1だから,x座標の差が2を探す)
P=5のとき,(5,3),(b,5)であるから,Q=4,6 (y座標の差が2だから,x座標の差が1を探す)
P=6のとき,(6,3),(b,6)で,このときは該当なし。
以上より,8通りなので,確率は1/3
問3 どの点が中心であるかを見抜けばよい。
(1)操作1ではFが中心となって90度回り,操作2ではEが中心となって90度回る。
Fが中心となる場合は半径が4,Eが中心となる場合は半径が4√2である。
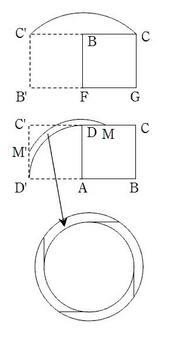
(2)操作 1:MとDは図のような線を描く。線分MDはまるで
屋根瓦のような形になる。MDの動く面積は,
(MDの長さ)×(弧CC'の長さ)であり,弧CC'の長さは
FC=4√2であることに注意して,
2×4√2×2×π×1/4=4√2π
操作 2 :MDが回転してできる部分は,下の図のとおり
であるが,これは,ドーナツ型の図のように4等分した
うちの1つになっている。
ドーナツ型の面積は(2√5)^2π-4^2π=4πであり,
その4等分したものはπ。
よって線分MDが動いた部分の合計は,4√2π+π
http://www.koukou.hokkaido-c.ed.jp/gakuryokukensa/gakuryoku.html
■■まとめ■■
最後の[6]が学校裁量の問題です。(3)は今まで,類題を経験したかどうかがカギになります。
■■ポイント■■
[1]→共通問題[2]と同じ。
[2]→共通問題[3]と同じ。
[3]→共通問題[4]と同じ。
[4]→共通問題[5]と同じ。
[5]→共通問題[6]と同じ。
[6]ここが応用問題になっている。
問1 式を作って因数分解して考える問題である。三平方の定理より,
a^2=b^2=(2√15)^2 であるからこれを式変形すると,
a^2-b^2=60 → (a+b)(a-b)=60。 つまり掛け算して60。
あとは,これをシラミツブシに探していく。
①a+b=60,a-b=1のとき, →2a=61でaが自然数にならない。
②a+b=30,a-b=2のとき,これを解くと,(a,b)=(16,14)
③a+b=20,a-b=3のとき, →2a=23でaが自然数にならない。
④a+b=15,a-b=4のとき, →2a=19でaが自然数にならない。
⑤a+b=12,a-b=5のとき, →2a=17でaが自然数にならない。
⑥a+b=10,a-b=6のとき,これを解くと,(a,b)=(8,2)
問2 とりあえず全部で24通りしかないので,丁寧にやっていけば答えにたどり着く。
長さが√5になる,ということは,x座標・y座標の差が1と2のときだけである。
P=1のとき,(1,3),(b,1)であるから,Q=0,2 (y座標の差が2だから,x座標の差が1を探す)
P=2のとき,(2,3),(b,2)であるから,Q=0,4 (y座標の差が1だから,x座標の差が2を探す)
P=3のとき,(3,3),(b,3)で,このときは該当なし。
P=4のとき,(4,3),(b,4)であるから,Q=2,6 (y座標の差が1だから,x座標の差が2を探す)
P=5のとき,(5,3),(b,5)であるから,Q=4,6 (y座標の差が2だから,x座標の差が1を探す)
P=6のとき,(6,3),(b,6)で,このときは該当なし。
以上より,8通りなので,確率は1/3
問3 どの点が中心であるかを見抜けばよい。
(1)操作1ではFが中心となって90度回り,操作2ではEが中心となって90度回る。
Fが中心となる場合は半径が4,Eが中心となる場合は半径が4√2である。
(2)操作 1:MとDは図のような線を描く。線分MDはまるで
屋根瓦のような形になる。MDの動く面積は,
(MDの長さ)×(弧CC'の長さ)であり,弧CC'の長さは
FC=4√2であることに注意して,
2×4√2×2×π×1/4=4√2π
操作 2 :MDが回転してできる部分は,下の図のとおり
であるが,これは,ドーナツ型の図のように4等分した
うちの1つになっている。
ドーナツ型の面積は(2√5)^2π-4^2π=4πであり,
その4等分したものはπ。
よって線分MDが動いた部分の合計は,4√2π+π
平成22年度・北海道(数学)高校入試問題 [平成22年度(2010年)・数学]
平成22年度・北海道(数学)高校入試問題のダウンロードはこちらから
http://www.koukou.hokkaido-c.ed.jp/gakuryokukensa/gakuryoku.html
■■まとめ■■
標準的な問題です。問題の難易がはっきりしています。
解ける問題から考えていきましょう。
★★つき問題は1つ。
●[4]問3.四角形の面積を求めるときの工夫の仕方を考えます。関数で面積を求める場合は,
軸に平行な方向の長さを考えることが大変多いです。
■■ポイント■■
[1]計算問題。難しいことはない。
問1(1)正負の計算。
(2)分数の計算。
(3)平方根の計算。この3問は取り立てて問題ない。
問2 式の値を求める問題は,まずは式変形してからその後代入をする。
-3xy^2にxとyを代入する。
問3 連立方程式。代入法でも加減法でもよい。
問4 yはxに反比例するからxy=aの形を使う。今回はx=3,y=-4を代入すると,
xy=-12で,比例定数は-12より。y=2を代入すると,x=-6
問5 斜めになっている平行四辺形だが,結局回転させるとへこんだ部分にとがった部分
がぴったりと入り込むことになるので,円柱の体積と同じになる。
[2]小問集合
問1 4本⇒AC,BDとAD中点・BC中点を通る線 と AB中点・DC中点を通る線
問2 樹形図を描く(全通り書いてみる)。数え漏れをなくすため,なるべく大きい順とか小さい順と
か,順番をつけて書く。
(50円,20円,10円)の順で小さい順に書く。
①50円が0のとき,
(0-0-8),(0-1-6),(0-2-4),(0-3-2),(0-4-1)
②50円が1のとき,
(1-0-3),(1-1-1)
このように全部で7通りある。よって見つけたもの以外に5通りある。
[3]方程式を作る問題
問1 問題文にこっそりと消しゴム1個がノートよりも40円安いことが書いてあるので,
5x+3(x-40)+980=2140 【方程式】
8x-120+980=2140 ⇒ 8x=1280 x=160円
弟から1000円預かったので(ややこしい!!)840円返す
問2.AR,BP,CQ=xとおけば,
△ABP=x×7÷2,△RQC=x×(7-x)÷2
この和が全体の4/7になる。
x×7÷2+x×(7-x)÷2 = 6×7÷2×4/7
7x+(7x-x^2)=24 → x^2-14x+24=0
→(x-2)(x-12)=0 であるから,x=2(cm)
[4]2次関数の問題。
問1 Aの座標は(-1,-1)となるので,
傾き2である直線はy=2(x+1)-1より,y=2x+1
問2 変域を考えると,x=-2のときy=8となるので,これをy=ax2に代入して,8=4a → a=2
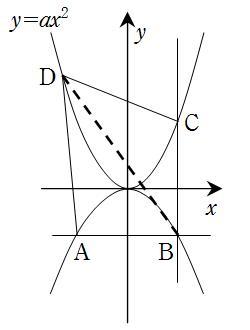
★問3 この問題は右のような図になっている。
四角形の面積を求めるときは,BDで2つに分
けると求めやすい。
A(-2,-4),B(2,-4),C(2,4a),
D(-3,9a)であるから,
△ABDは底辺AB(=4)とすると
高さは9a-(-4)=9a+4。
△CBDは底辺BC(=4a-(-4)=4a+4)とすると,高さは5より,
(四角形ABCD)=4×(9a+4)÷2+(4a+4)×5÷2 =25
(36a+16)+(20a+20)=50 → a=1/4
[5]図形の作図に関する問題
問1 右上方向,左上方向,下方向に平行四辺形が伸びる。
問2 二等辺三角形において,頂角の二等分線は底辺を垂直二等分する,という知識を使う。
(証明)まずは△APB≡△AQBを示す。
AP=AQ(円Aの半径),BP=BQ(円Bの半径)であり,辺ABは共通。
よって,3辺がそれぞれ等しいので,△APB≡△AQBである。
これより,∠PAB=∠QABがいえる。…①
すると,二等辺三角形APQにおいて①が成立するので直線ABは角の二等分線になっている。
つまりこの線は底辺を垂直に二等分する直線である。
[6]図形に関する問題の集合。
問1 111°という中途半端な角度は何であるかを考えると,まず∠C=72°であり,∠Aの78を2で割る
と39°。つまり,∠Aの半分と∠Cを加えると111°となるので,∠Aの二等分線を引き,∠Cと加え
る外角を考えればよい。
問2 CEとPDの交点をRとすると,△PBD∽△RCDより,PBの長さの半分がCRになるから,CR=3。
△APQ∽△CRQで,相似比はAP:CR=2:3よって,AQ:QC=2:3からQCを求める。
問3 点PはOC上にあるので,面OACを取り出して考える。
あとは,△OMCの面積を2通りで表す,という方法で考えるか,
相似な三角形を使って求めてもよい。
◆◆入試過去問購入はこちら◆◆
http://www.koukou.hokkaido-c.ed.jp/gakuryokukensa/gakuryoku.html
■■まとめ■■
標準的な問題です。問題の難易がはっきりしています。
解ける問題から考えていきましょう。
★★つき問題は1つ。
●[4]問3.四角形の面積を求めるときの工夫の仕方を考えます。関数で面積を求める場合は,
軸に平行な方向の長さを考えることが大変多いです。
■■ポイント■■
[1]計算問題。難しいことはない。
問1(1)正負の計算。
(2)分数の計算。
(3)平方根の計算。この3問は取り立てて問題ない。
問2 式の値を求める問題は,まずは式変形してからその後代入をする。
-3xy^2にxとyを代入する。
問3 連立方程式。代入法でも加減法でもよい。
問4 yはxに反比例するからxy=aの形を使う。今回はx=3,y=-4を代入すると,
xy=-12で,比例定数は-12より。y=2を代入すると,x=-6
問5 斜めになっている平行四辺形だが,結局回転させるとへこんだ部分にとがった部分
がぴったりと入り込むことになるので,円柱の体積と同じになる。
[2]小問集合
問1 4本⇒AC,BDとAD中点・BC中点を通る線 と AB中点・DC中点を通る線
問2 樹形図を描く(全通り書いてみる)。数え漏れをなくすため,なるべく大きい順とか小さい順と
か,順番をつけて書く。
(50円,20円,10円)の順で小さい順に書く。
①50円が0のとき,
(0-0-8),(0-1-6),(0-2-4),(0-3-2),(0-4-1)
②50円が1のとき,
(1-0-3),(1-1-1)
このように全部で7通りある。よって見つけたもの以外に5通りある。
[3]方程式を作る問題
問1 問題文にこっそりと消しゴム1個がノートよりも40円安いことが書いてあるので,
5x+3(x-40)+980=2140 【方程式】
8x-120+980=2140 ⇒ 8x=1280 x=160円
弟から1000円預かったので(ややこしい!!)840円返す
問2.AR,BP,CQ=xとおけば,
△ABP=x×7÷2,△RQC=x×(7-x)÷2
この和が全体の4/7になる。
x×7÷2+x×(7-x)÷2 = 6×7÷2×4/7
7x+(7x-x^2)=24 → x^2-14x+24=0
→(x-2)(x-12)=0 であるから,x=2(cm)
[4]2次関数の問題。
問1 Aの座標は(-1,-1)となるので,
傾き2である直線はy=2(x+1)-1より,y=2x+1
問2 変域を考えると,x=-2のときy=8となるので,これをy=ax2に代入して,8=4a → a=2
★問3 この問題は右のような図になっている。
四角形の面積を求めるときは,BDで2つに分
けると求めやすい。
A(-2,-4),B(2,-4),C(2,4a),
D(-3,9a)であるから,
△ABDは底辺AB(=4)とすると
高さは9a-(-4)=9a+4。
△CBDは底辺BC(=4a-(-4)=4a+4)とすると,高さは5より,
(四角形ABCD)=4×(9a+4)÷2+(4a+4)×5÷2 =25
(36a+16)+(20a+20)=50 → a=1/4
[5]図形の作図に関する問題
問1 右上方向,左上方向,下方向に平行四辺形が伸びる。
問2 二等辺三角形において,頂角の二等分線は底辺を垂直二等分する,という知識を使う。
(証明)まずは△APB≡△AQBを示す。
AP=AQ(円Aの半径),BP=BQ(円Bの半径)であり,辺ABは共通。
よって,3辺がそれぞれ等しいので,△APB≡△AQBである。
これより,∠PAB=∠QABがいえる。…①
すると,二等辺三角形APQにおいて①が成立するので直線ABは角の二等分線になっている。
つまりこの線は底辺を垂直に二等分する直線である。
[6]図形に関する問題の集合。
問1 111°という中途半端な角度は何であるかを考えると,まず∠C=72°であり,∠Aの78を2で割る
と39°。つまり,∠Aの半分と∠Cを加えると111°となるので,∠Aの二等分線を引き,∠Cと加え
る外角を考えればよい。
問2 CEとPDの交点をRとすると,△PBD∽△RCDより,PBの長さの半分がCRになるから,CR=3。
△APQ∽△CRQで,相似比はAP:CR=2:3よって,AQ:QC=2:3からQCを求める。
問3 点PはOC上にあるので,面OACを取り出して考える。
あとは,△OMCの面積を2通りで表す,という方法で考えるか,
相似な三角形を使って求めてもよい。
◆◆入試過去問購入はこちら◆◆



