平成23年度・沖縄県(数学)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・沖縄県(数学)高校入試問題のダウンロードはこちらから
私塾につながるためリンク先を明示いたしません。ご了承ください。
■■まとめ■■
例年通りの形式です。問題集が多めだと感じます。所々難しい問題があり,空間の最後などは考えにくかったでしょう。できるところからやるとよいでしょう。
■■解説■■
クリックすると大きくなります。参考にしてください。



■■ポイント■■
[1]計算問題
ここは問題ないだろう。
[2]小問集合
(1)7x-4=5x+6 → 2x=10 → x=5
(2)(3x+1)2=9x2+6x+1
(3)x2+x-6=(x+3)(x-2)
(4)連立方程式
(5)10a+b
(6)2x+5y-3=0 →2x+5y=3 → yについて得。
(7)√10は見た段階で3とわかるが,一応3.5^2=12.25であるから,√10は3.5よりも小さい数
であるとわかる。よって3が一番近い。
(8)展開しないこと。
(x-4)2=6 → x-4=±√6 → x=4±√6
(9)3(x-2y)-(2x-5y)=x-yであるから,ここで代入して,-2-3=-5
(10)90×0.43=38.7分である。0.7分は0.7×60=42秒であるから,合計38分42秒
[3]図形を回転させたときにできる図形の問題。
(1)対角線は1,2,√5の四角形である。
(2)図のような形になる。弧AA'の部分が一番重要で,ここは半径√5の円の1/4になることに
注意する。
[4]作図の問題。
ABを直径とする円を書き,円の弧上に点Pをとればそれがすべて直角三角形になる。
[5]グラフと方程式の問題。
(1)Aさんは1分間で250m走るので,y=250x
(2)1分間で50mの差がつく。400m分の差がつくのは400÷50=8分後
(3)Cさんは4000m走った。Aさんと同じ速さをa周,Bさんと同じ速さをb周とすると,
連立方程式を作ればよい。
[6]2次関数の問題。(3)も頻出か。
(1)2次関数の変域は,原点を通過するときに注意すればよい。x=4のときyが最大になる。
よって,0≦y≦8
(2)傾きと切片の公式から解く。y=x+4
(3)平行四辺形の面積を二等分するとき,平行四辺形の対角線の交点(=対角線の中点)を
通る。B(4,8)だからC(0,8)で,D(2,2)に注意すると,CDの中点はM(1,5)であるから,
原点と(1,5)を通る直線の式はy=5x
[7]とりあえずさいころが2つなので,全部の場合の数は36通り。あとは丁寧にやっていく。
(1)F→C→Eの順でコマの位置が変わる。
(2)2回で終了するときは,
(1,6)(2,5)(3,4)(4,3)(5,2)(6,1)の全6通り。
(3)これも丁寧に数え上げればよい。
(1,5)(2,4)(3,3)(4,2)(5,1)
(2,6)(3,5)(4,4)(5,3)(6,2)の10通り。
[8]弧の長さと円周角の比の問題。
(1)△ABGと△EDGで,
∠Gは対頂角で等しい。…①
弧AEに対する円周角は等しいので,
∠ABG=∠EDG…②
①・②より,2角が等しいので,
△ABG∽△EDG
(2)∠BAC=17°で,BE//DEであるから,弧DEに対する円周角も17°。また∠AEB=67°を図の
ように書き込む。∠AGEは(※)アルハゼンの定理より弧AEと弧BDの円周角の和になるので,
180-(67+17)=96°
(※)アルハゼンの定理がわからない方は,私のHPの左側に動画解説のリンクがあります
ので,ぜひご覧ください。
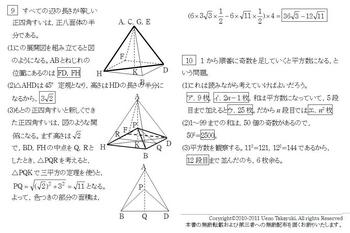
[9]すべての辺の長さが等しい正四角すいは,正八面体の半分である。
(1)この展開図を組み立てると図のようになる。ABとねじれの位置にあるのはFD,FH
(2)△AHDは45°定規となり,高さはHDの長さの半分になる。
(3)もとの正四角すいと新しくできた正四角すいは,図のような関係になる。
D,FHの中点をQ,Rとしたとき,△PQRを考えると,△PQKで三平方の定理を使うと,
√11となる。あとは色つき部分の面積を求める。
[10]1から順番に奇数を足していくと平方数になる,という問題。
(1)これは読みながら考えていけばよいだろう。
ア.9枚,イ.2n-1枚,和は平方数になっていて,5段目まで加えるとウ.25枚。
だからn段目ではエ.n2枚
(2)1~99までの和は,50個の奇数があるので,50^2=2500。
(3)平方数を観察する。112=121,122=144であるから,12段目まで並んだのち,6枚余る。
私塾につながるためリンク先を明示いたしません。ご了承ください。
■■まとめ■■
例年通りの形式です。問題集が多めだと感じます。所々難しい問題があり,空間の最後などは考えにくかったでしょう。できるところからやるとよいでしょう。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]計算問題
ここは問題ないだろう。
[2]小問集合
(1)7x-4=5x+6 → 2x=10 → x=5
(2)(3x+1)2=9x2+6x+1
(3)x2+x-6=(x+3)(x-2)
(4)連立方程式
(5)10a+b
(6)2x+5y-3=0 →2x+5y=3 → yについて得。
(7)√10は見た段階で3とわかるが,一応3.5^2=12.25であるから,√10は3.5よりも小さい数
であるとわかる。よって3が一番近い。
(8)展開しないこと。
(x-4)2=6 → x-4=±√6 → x=4±√6
(9)3(x-2y)-(2x-5y)=x-yであるから,ここで代入して,-2-3=-5
(10)90×0.43=38.7分である。0.7分は0.7×60=42秒であるから,合計38分42秒
[3]図形を回転させたときにできる図形の問題。
(1)対角線は1,2,√5の四角形である。
(2)図のような形になる。弧AA'の部分が一番重要で,ここは半径√5の円の1/4になることに
注意する。
[4]作図の問題。
ABを直径とする円を書き,円の弧上に点Pをとればそれがすべて直角三角形になる。
[5]グラフと方程式の問題。
(1)Aさんは1分間で250m走るので,y=250x
(2)1分間で50mの差がつく。400m分の差がつくのは400÷50=8分後
(3)Cさんは4000m走った。Aさんと同じ速さをa周,Bさんと同じ速さをb周とすると,
連立方程式を作ればよい。
[6]2次関数の問題。(3)も頻出か。
(1)2次関数の変域は,原点を通過するときに注意すればよい。x=4のときyが最大になる。
よって,0≦y≦8
(2)傾きと切片の公式から解く。y=x+4
(3)平行四辺形の面積を二等分するとき,平行四辺形の対角線の交点(=対角線の中点)を
通る。B(4,8)だからC(0,8)で,D(2,2)に注意すると,CDの中点はM(1,5)であるから,
原点と(1,5)を通る直線の式はy=5x
[7]とりあえずさいころが2つなので,全部の場合の数は36通り。あとは丁寧にやっていく。
(1)F→C→Eの順でコマの位置が変わる。
(2)2回で終了するときは,
(1,6)(2,5)(3,4)(4,3)(5,2)(6,1)の全6通り。
(3)これも丁寧に数え上げればよい。
(1,5)(2,4)(3,3)(4,2)(5,1)
(2,6)(3,5)(4,4)(5,3)(6,2)の10通り。
[8]弧の長さと円周角の比の問題。
(1)△ABGと△EDGで,
∠Gは対頂角で等しい。…①
弧AEに対する円周角は等しいので,
∠ABG=∠EDG…②
①・②より,2角が等しいので,
△ABG∽△EDG
(2)∠BAC=17°で,BE//DEであるから,弧DEに対する円周角も17°。また∠AEB=67°を図の
ように書き込む。∠AGEは(※)アルハゼンの定理より弧AEと弧BDの円周角の和になるので,
180-(67+17)=96°
(※)アルハゼンの定理がわからない方は,私のHPの左側に動画解説のリンクがあります
ので,ぜひご覧ください。
[9]すべての辺の長さが等しい正四角すいは,正八面体の半分である。
(1)この展開図を組み立てると図のようになる。ABとねじれの位置にあるのはFD,FH
(2)△AHDは45°定規となり,高さはHDの長さの半分になる。
(3)もとの正四角すいと新しくできた正四角すいは,図のような関係になる。
D,FHの中点をQ,Rとしたとき,△PQRを考えると,△PQKで三平方の定理を使うと,
√11となる。あとは色つき部分の面積を求める。
[10]1から順番に奇数を足していくと平方数になる,という問題。
(1)これは読みながら考えていけばよいだろう。
ア.9枚,イ.2n-1枚,和は平方数になっていて,5段目まで加えるとウ.25枚。
だからn段目ではエ.n2枚
(2)1~99までの和は,50個の奇数があるので,50^2=2500。
(3)平方数を観察する。112=121,122=144であるから,12段目まで並んだのち,6枚余る。
平成23年度・群馬県(数学)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・群馬県(数学)高校入試問題のダウンロードはこちらから
http://www.tokyo-np.co.jp/k-shiken/index.html
■■まとめ■■
例年通りの形式です。[4]のグラフをかく問題,[5]の相似を見つける問題がちょっと難しかったかもしれません。差がつく問題になったことでしょう。
■■解説■■
クリックすると大きくなります。参考にしてください。



■■ポイント■■
[1]計算問題
計算問題はぜひ完答してほしい問題である。
[2]小問集合
(1)五角形の内角の和:五角形は三角形が3枚あると考えて,540°
(2)一番上の列と一番左の列を比べて,a-3+4=a+3+b。これよりb=-2
斜めの列と一番上の列を見比べて,4+1-2=4-3+a これよりa=2
(3)2x2y-10xy-12yはまず2yが共通因数だから,=2y(x2-5y-6)=2y(x-6)(x+1)
(4)①yをxの式で表すと,y=ax2となり,(2,6)を代入すると,6=4a。よって,a=3/2。
②2秒後から4秒後まででは,2秒の時は6mの位置に,4秒の時は24mの位置にいるから,18m
(5)この問題は組み合わせの考え方を使う。全部の場合の数は6つの玉から2つの玉をとる
組み合わせなので,(6×5)÷(2×1)=15通り。このうち,色が同じ場合は,
赤2個:(3×2)÷(2×1)=3通り,白2個:(2×1)÷(2×1)=1通りあるから,全部で4通り。
よって異なる場合の確率は,11/15
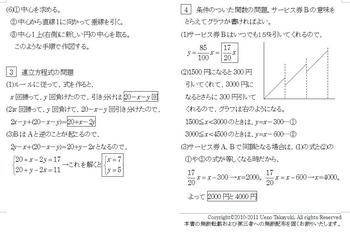
(6)①中心を求める。
②中心から直線lに向かって垂線を引く。
③中心l上(右側)に新しい円の中心を取る。このような手順で作図する。
[3]連立方程式の問題
(1)ルールに従って,式を作ると,x回勝って,y回負けたので,引き分けは20-x-y回
(2)x回勝って,y回負けて,20-x-y回引き分けたので,2x-y+(20-x-y)=20+x-2y
(3)BはAと逆のことが起こるので,2y-x+(20-x-y)=20+y-2xとなるので,
{ 20+x-2y=17 →これを解くと x=7,y=5
20+y-2x=11
[4]条件のついた関数の問題。サービス券Bの意味をとらえてグラフが書ければよい。
(1)サービス券Bはいつでも15%引いてくれるので,y=85x/100=17x/20
(2)1500円になると300円引いてくれて,3000円になるとさらに300円引いてくれる。
1500≦x<3000のときは,y=x-300…①
3000≦x<4500のときは,y=x-600…②
(3)サービス券A,Bで同額となる場合は,(1)の式と(2)の①や②の式が等しくなる時だから,
x-300=17x/20→x=2000。
x-600=17x/20→x=4000。よって2000円と4000円
[5]平面図形の相似の問題。最後が私立校入試の問題のようである。
(1)△AEHと△BECにおいて,
∠AEH=∠BEC=90°…①
△AEBで∠A=45°,∠AEBは90°だから△AEBは直角二等辺三角形で,AE=BE…②
ここで,△AEHと△BDHは∠Hが対頂角,∠E=∠D=90°で等しいので,
△AEH∽△BDHよって∠EAH=∠EBC…③
①~③より1辺とその両端の角が等しいので,△AEH≡△BEC。
これより対応する辺の長さが等しいのでAH=BC。
(2)(3)AH=4であり,(3)で求めたいHDをxと置く。すると図で●を
含む直角三角形は全て相似になるから,
△BDH∽△BEC∽△AEH∽△ADC
ここで長さを埋めていくと,
△BDHと△ADCで3:x=4+x:1 という式ができる。
これより,x(4+x)=3 → x2+4x-3=0。x=-2+√7
。AD=4+x=2+√7であるから,
△ABCの面積S=4×(2+√7)×1/2=4+2√7
[6]空間図形。相似比と体積比の考え方を使う。すべての辺の長さが等しい四角すいはよく
出てくる。
(1)△ABDを考えると,BD=8√2である45°定規になっているから,高さは4√2
(2)半分の高さまで水が入っている,ということは,水が入っていない部分の小さな四角すい
と全体の四角すいが相似で,相似比が1:2だから,体積比は1:8。
よって全体:下側の体積比は8:7
(3)①図IIのようになったとき,底面となるEBCD:FBCG=8:7となる。よってCD:CG=8:7である
から,CG=7
②二等辺三角形の絵を2つ書く。
図のように△ACDと△AGFを考える。△ACDは正三角形であるから,AG=√57
また,右の図で,AQ=√41
これよりS=8×√41×1/2=4√41
http://www.tokyo-np.co.jp/k-shiken/index.html
■■まとめ■■
例年通りの形式です。[4]のグラフをかく問題,[5]の相似を見つける問題がちょっと難しかったかもしれません。差がつく問題になったことでしょう。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]計算問題
計算問題はぜひ完答してほしい問題である。
[2]小問集合
(1)五角形の内角の和:五角形は三角形が3枚あると考えて,540°
(2)一番上の列と一番左の列を比べて,a-3+4=a+3+b。これよりb=-2
斜めの列と一番上の列を見比べて,4+1-2=4-3+a これよりa=2
(3)2x2y-10xy-12yはまず2yが共通因数だから,=2y(x2-5y-6)=2y(x-6)(x+1)
(4)①yをxの式で表すと,y=ax2となり,(2,6)を代入すると,6=4a。よって,a=3/2。
②2秒後から4秒後まででは,2秒の時は6mの位置に,4秒の時は24mの位置にいるから,18m
(5)この問題は組み合わせの考え方を使う。全部の場合の数は6つの玉から2つの玉をとる
組み合わせなので,(6×5)÷(2×1)=15通り。このうち,色が同じ場合は,
赤2個:(3×2)÷(2×1)=3通り,白2個:(2×1)÷(2×1)=1通りあるから,全部で4通り。
よって異なる場合の確率は,11/15
(6)①中心を求める。
②中心から直線lに向かって垂線を引く。
③中心l上(右側)に新しい円の中心を取る。このような手順で作図する。
[3]連立方程式の問題
(1)ルールに従って,式を作ると,x回勝って,y回負けたので,引き分けは20-x-y回
(2)x回勝って,y回負けて,20-x-y回引き分けたので,2x-y+(20-x-y)=20+x-2y
(3)BはAと逆のことが起こるので,2y-x+(20-x-y)=20+y-2xとなるので,
{ 20+x-2y=17 →これを解くと x=7,y=5
20+y-2x=11
[4]条件のついた関数の問題。サービス券Bの意味をとらえてグラフが書ければよい。
(1)サービス券Bはいつでも15%引いてくれるので,y=85x/100=17x/20
(2)1500円になると300円引いてくれて,3000円になるとさらに300円引いてくれる。
1500≦x<3000のときは,y=x-300…①
3000≦x<4500のときは,y=x-600…②
(3)サービス券A,Bで同額となる場合は,(1)の式と(2)の①や②の式が等しくなる時だから,
x-300=17x/20→x=2000。
x-600=17x/20→x=4000。よって2000円と4000円
[5]平面図形の相似の問題。最後が私立校入試の問題のようである。
(1)△AEHと△BECにおいて,
∠AEH=∠BEC=90°…①
△AEBで∠A=45°,∠AEBは90°だから△AEBは直角二等辺三角形で,AE=BE…②
ここで,△AEHと△BDHは∠Hが対頂角,∠E=∠D=90°で等しいので,
△AEH∽△BDHよって∠EAH=∠EBC…③
①~③より1辺とその両端の角が等しいので,△AEH≡△BEC。
これより対応する辺の長さが等しいのでAH=BC。
(2)(3)AH=4であり,(3)で求めたいHDをxと置く。すると図で●を
含む直角三角形は全て相似になるから,
△BDH∽△BEC∽△AEH∽△ADC
ここで長さを埋めていくと,
△BDHと△ADCで3:x=4+x:1 という式ができる。
これより,x(4+x)=3 → x2+4x-3=0。x=-2+√7
。AD=4+x=2+√7であるから,
△ABCの面積S=4×(2+√7)×1/2=4+2√7
[6]空間図形。相似比と体積比の考え方を使う。すべての辺の長さが等しい四角すいはよく
出てくる。
(1)△ABDを考えると,BD=8√2である45°定規になっているから,高さは4√2
(2)半分の高さまで水が入っている,ということは,水が入っていない部分の小さな四角すい
と全体の四角すいが相似で,相似比が1:2だから,体積比は1:8。
よって全体:下側の体積比は8:7
(3)①図IIのようになったとき,底面となるEBCD:FBCG=8:7となる。よってCD:CG=8:7である
から,CG=7
②二等辺三角形の絵を2つ書く。
図のように△ACDと△AGFを考える。△ACDは正三角形であるから,AG=√57
また,右の図で,AQ=√41
これよりS=8×√41×1/2=4√41
平成23年度・高知県後期(数学応用)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・高知県後期(数学応用)高校入試問題のダウンロードはこちらから
http://www.pref.kochi.lg.jp/soshiki/311701/mondai.html
■■まとめ■■
基礎問題と共通の問題も多いです。基本的な問題が並んでいます。
[4]の最後が考えにくいでしょう。4つ全て見つけるのはちょっと難しいかと思います。
■■解説■■
クリックすると大きくなります。参考にしてください。


■■ポイント■■
[1]計算問題。
(1)5×(-3)2-23=45-8=37
(2)分数の計算
(3)文字式の計算。
(4)(x+2y)2-(x-2y)2=x2+4xy+4y2-x2+4xy-4y2=8xy
(5)√が消える計算。
[2]小問集合
(1)-50/7は-7.1…,13/8=1.5…より,-7から1まで計9個
(2)等式変形は図参照
(3)連立方程式を作る。男子x人,女子y人として,
{x+y=480
-2/100x + 5/100y=10 と変形。
これより,x=200人,(y=280人)
(4)y=ax^2で,x=-3のときy=2を代入すると,a=2/9。ここで,x=-2を代入する。
(5)ABを軸として回転させるとき,大きい円柱から内側にできた,円すいを引けばよい。
円柱:10×10×π×23=2300π
円すい:10×10×π×9×1/3=300π。よって2000π
(6)1000個中2個が不良品であったから,比を考えると,1000:2=x:30。
これより,x=15000個
[3]グラフを読みこなせばよい。
(1)傾きを求めると,24であり,(8,256)を通るので,直線の公式に代入して,
y=24(x-8)+256。→y=24x+64
(2)(1)でy=480を代入して,480=24x+64。24x=416→x=52/3→17分20秒
(3)A,B同時に入れるときは,毎分32lずつ入る。
よって,640l入れるには640÷32=20分かかる。
[4]丁寧に図を書けばよい。(3)はちょっと難しいか。
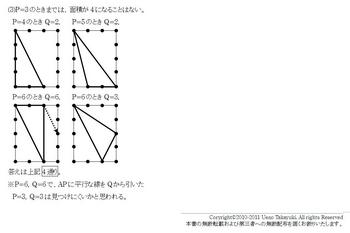
(1)1回目3,2回目5のとき,図のようになる。
(2)一直線上に並ぶときは,線分AB上にいるときしかない。
P=1のとき(1,1)(1,2)(1,3)
P=2のとき(2,1)(2,2)
P=3のとき(3,1)。合計6通り
(3)P=3のときまでは,面積が4になることはない。
P=4のときQ=2,P=5のときQ=2,
P=6のときQ=6,P=6のときQ=3,
答えは上記4通り。
※P=6,Q=6で,APに平行な線をQから引いたP=3,Q=3は見つけにくいかと思われる。
http://www.pref.kochi.lg.jp/soshiki/311701/mondai.html
■■まとめ■■
基礎問題と共通の問題も多いです。基本的な問題が並んでいます。
[4]の最後が考えにくいでしょう。4つ全て見つけるのはちょっと難しいかと思います。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]計算問題。
(1)5×(-3)2-23=45-8=37
(2)分数の計算
(3)文字式の計算。
(4)(x+2y)2-(x-2y)2=x2+4xy+4y2-x2+4xy-4y2=8xy
(5)√が消える計算。
[2]小問集合
(1)-50/7は-7.1…,13/8=1.5…より,-7から1まで計9個
(2)等式変形は図参照
(3)連立方程式を作る。男子x人,女子y人として,
{x+y=480
-2/100x + 5/100y=10 と変形。
これより,x=200人,(y=280人)
(4)y=ax^2で,x=-3のときy=2を代入すると,a=2/9。ここで,x=-2を代入する。
(5)ABを軸として回転させるとき,大きい円柱から内側にできた,円すいを引けばよい。
円柱:10×10×π×23=2300π
円すい:10×10×π×9×1/3=300π。よって2000π
(6)1000個中2個が不良品であったから,比を考えると,1000:2=x:30。
これより,x=15000個
[3]グラフを読みこなせばよい。
(1)傾きを求めると,24であり,(8,256)を通るので,直線の公式に代入して,
y=24(x-8)+256。→y=24x+64
(2)(1)でy=480を代入して,480=24x+64。24x=416→x=52/3→17分20秒
(3)A,B同時に入れるときは,毎分32lずつ入る。
よって,640l入れるには640÷32=20分かかる。
[4]丁寧に図を書けばよい。(3)はちょっと難しいか。
(1)1回目3,2回目5のとき,図のようになる。
(2)一直線上に並ぶときは,線分AB上にいるときしかない。
P=1のとき(1,1)(1,2)(1,3)
P=2のとき(2,1)(2,2)
P=3のとき(3,1)。合計6通り
(3)P=3のときまでは,面積が4になることはない。
P=4のときQ=2,P=5のときQ=2,
P=6のときQ=6,P=6のときQ=3,
答えは上記4通り。
※P=6,Q=6で,APに平行な線をQから引いたP=3,Q=3は見つけにくいかと思われる。
平成23年度・高知県後期(数学基礎)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・高知県後期(数学基礎)高校入試問題のダウンロードはこちらから
http://www.pref.kochi.lg.jp/soshiki/311701/mondai.html
■■まとめ■■
特に難しい問題はありません。時間をよく見ながら完答を目指しましょう。
応用と同じ問題も多く含まれます。
■■解説■■
クリックすると大きくなります。参考にしてください。

■■ポイント■■
[1]計算問題。
(1)8-(-5)=13
(2)24÷(-3)=-8
(3)(-2)×4+12÷3=-8+4=-4
(4)分数の計算
(5)12a^3b÷2ab=6a^2
(6)(2a)^2÷6a^3×3a^2=4a^2÷6a^3×3a^2=2a
(7)(x+1)^2+x(x-2)=x^2+2x+1+x^2-2x=2x^2+1
(8)√の計算
[2]応用と同一問題。
[3](1)(2)は応用と同一問題。
[4](1)(2)は応用と同一問題。
http://www.pref.kochi.lg.jp/soshiki/311701/mondai.html
■■まとめ■■
特に難しい問題はありません。時間をよく見ながら完答を目指しましょう。
応用と同じ問題も多く含まれます。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]計算問題。
(1)8-(-5)=13
(2)24÷(-3)=-8
(3)(-2)×4+12÷3=-8+4=-4
(4)分数の計算
(5)12a^3b÷2ab=6a^2
(6)(2a)^2÷6a^3×3a^2=4a^2÷6a^3×3a^2=2a
(7)(x+1)^2+x(x-2)=x^2+2x+1+x^2-2x=2x^2+1
(8)√の計算
[2]応用と同一問題。
[3](1)(2)は応用と同一問題。
[4](1)(2)は応用と同一問題。
平成23年度・岡山朝日高校(数学)入試問題 [平成23年度(2011年)・数学]
平成23年度・岡山朝日高校(数学)入試問題のダウンロードはこちらから
http://kenjukuren.moo.jp/QandA.htm
■■まとめ■■
[1]~[3]までは比較的易しめでここは全問正解してほしいところではあります。[4][5]については,簡単な問題と考えにくい問題が混ざっていますが,問題自体は素直な問題が並んでいますので,しっかりと学習してきた生徒にとっては適切な問題だったでしょう。
■■解説■■
クリックすると大きくなります。参考にしてください。

■■ポイント■■
[1]計算と小問。
①複雑な式ではあるが,難しくはない。
②a^2-2a-8=(a-4)(a+2)と因数分解できるので,ここで代入する。
③この双曲線はx=1のとき,y=8とわかる。よって比例定数をaとして,xy=8。よってb=2。
④和が4の倍数となるとき,
1.和が4→(1,3)(2,2)(3,1)
2.和が8→(2,6)(3,5)(4,4)(5,3)(6,2)
3.和が12→(6,6)。よって9通り。
積が4の倍数になるときは,1つ目の数が1~6について丁寧に考える。
(1,4),(2,2)(2,4)(2,6),(3,4),(4,1)~(4,6)の6通り,
(5,4),(6,2)(6,4)(6,6)。よって15通り。
⑤正五角形に対角線を引いてできる角は,36°,72°,108°の3種類で,すべて36の倍数
である。∠CAD=36°
[2]連立方程式の問題。条件にしたがって式を作る。
男子x人,女子y人として,
{x+y=108
7/10x+13/16y=108×3/4 →解いて x=60,y=48
[3]線分の中点は垂直二等分線を作図すればよい。中点をMとして,MAを半径とする円を書
き,垂直二等分線との交点をPとすれば,AP=BPの直角二等辺三角形が書ける。
[4]相似比と線分比の問題。
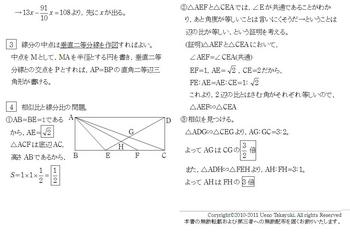
①AB=BE=1であるから,AE=√2
△ACFは底辺AC,高さABであるから,面積も求められる。
②△AEFと△CEAでは,∠Eが共通であることがわかり,あと角度が等しいことは言いにく
そうだ→ということは辺の比が等しい,という証明を考える。
(証明)△AEFと△CEAにおいて,
∠AEF=∠CEA(共通)
EF=1,AE=√2,CE=2だから,
FE:AE=AE:CE=1:√2
これより,2辺の比とはさむ角がそれぞれ等しいので,
△AEF∽△CEA
③相似を見つける。
△ADG∽△CEGより,AG:GC=3:2。よってAGはCGの3/2倍
また,△ADH∽△FEHより,AH:FH=3:1。よってAHはFHの3倍
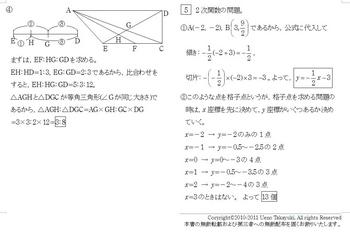
④まずは,EF:HG:GDを求める。
EH:HD=1:3,EG:GD=2:3であるから,比合わせをすると,EH:HG:GD=5:3:12。
△AGHと△DGCが等角三角形(∠Gが同じ大きさ)であるから,△AGH:△DGC=AG×GH:GC×DG
=3×3:2×12=3:8
[5]2次関数の問題。
①A(-2,-2),B(3,-9/2) であるから,公式に代入して
傾き:-1/2×(-2+3),切片:-(-1/2)×(-2)×+3=-3。
②このような点を格子点というが,格子点を求める問題の時は,x座標を先に決めて,y座標が
いくつあるか決めていく。
x=-2 → y=-2のみの1点
x=-1 → y=-0.5~-2.5の2点
x=0 → y=0~-3の4点
x=1 → y=-0.5~-3.5の3点
x=2 → y=-2~-4の3点
x=3のときはない。 よって13個
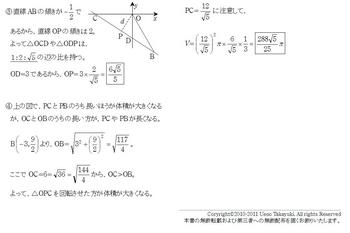
③直線ABの傾きが-1/2であるから,直線OPの傾きは2。
よって△OCDや△ODPは,1:2:√5の辺の比を持つ。
OD=3であるから,OP=3×2/√5 = 6√5/5
④PCとPBのうち長いほうが体積が大きくなるが,OCとOBのうちの長い方が,PCやPBが長くなる。
計算するとOC>OB。
よって,△OPCを回転させた方が体積が大きくなる。
PC=12/√5 に注意して,
V=(12/√5)^2×π×6/√5×1/3 という計算になる。
http://kenjukuren.moo.jp/QandA.htm
■■まとめ■■
[1]~[3]までは比較的易しめでここは全問正解してほしいところではあります。[4][5]については,簡単な問題と考えにくい問題が混ざっていますが,問題自体は素直な問題が並んでいますので,しっかりと学習してきた生徒にとっては適切な問題だったでしょう。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]計算と小問。
①複雑な式ではあるが,難しくはない。
②a^2-2a-8=(a-4)(a+2)と因数分解できるので,ここで代入する。
③この双曲線はx=1のとき,y=8とわかる。よって比例定数をaとして,xy=8。よってb=2。
④和が4の倍数となるとき,
1.和が4→(1,3)(2,2)(3,1)
2.和が8→(2,6)(3,5)(4,4)(5,3)(6,2)
3.和が12→(6,6)。よって9通り。
積が4の倍数になるときは,1つ目の数が1~6について丁寧に考える。
(1,4),(2,2)(2,4)(2,6),(3,4),(4,1)~(4,6)の6通り,
(5,4),(6,2)(6,4)(6,6)。よって15通り。
⑤正五角形に対角線を引いてできる角は,36°,72°,108°の3種類で,すべて36の倍数
である。∠CAD=36°
[2]連立方程式の問題。条件にしたがって式を作る。
男子x人,女子y人として,
{x+y=108
7/10x+13/16y=108×3/4 →解いて x=60,y=48
[3]線分の中点は垂直二等分線を作図すればよい。中点をMとして,MAを半径とする円を書
き,垂直二等分線との交点をPとすれば,AP=BPの直角二等辺三角形が書ける。
[4]相似比と線分比の問題。
①AB=BE=1であるから,AE=√2
△ACFは底辺AC,高さABであるから,面積も求められる。
②△AEFと△CEAでは,∠Eが共通であることがわかり,あと角度が等しいことは言いにく
そうだ→ということは辺の比が等しい,という証明を考える。
(証明)△AEFと△CEAにおいて,
∠AEF=∠CEA(共通)
EF=1,AE=√2,CE=2だから,
FE:AE=AE:CE=1:√2
これより,2辺の比とはさむ角がそれぞれ等しいので,
△AEF∽△CEA
③相似を見つける。
△ADG∽△CEGより,AG:GC=3:2。よってAGはCGの3/2倍
また,△ADH∽△FEHより,AH:FH=3:1。よってAHはFHの3倍
④まずは,EF:HG:GDを求める。
EH:HD=1:3,EG:GD=2:3であるから,比合わせをすると,EH:HG:GD=5:3:12。
△AGHと△DGCが等角三角形(∠Gが同じ大きさ)であるから,△AGH:△DGC=AG×GH:GC×DG
=3×3:2×12=3:8
[5]2次関数の問題。
①A(-2,-2),B(3,-9/2) であるから,公式に代入して
傾き:-1/2×(-2+3),切片:-(-1/2)×(-2)×+3=-3。
②このような点を格子点というが,格子点を求める問題の時は,x座標を先に決めて,y座標が
いくつあるか決めていく。
x=-2 → y=-2のみの1点
x=-1 → y=-0.5~-2.5の2点
x=0 → y=0~-3の4点
x=1 → y=-0.5~-3.5の3点
x=2 → y=-2~-4の3点
x=3のときはない。 よって13個
③直線ABの傾きが-1/2であるから,直線OPの傾きは2。
よって△OCDや△ODPは,1:2:√5の辺の比を持つ。
OD=3であるから,OP=3×2/√5 = 6√5/5
④PCとPBのうち長いほうが体積が大きくなるが,OCとOBのうちの長い方が,PCやPBが長くなる。
計算するとOC>OB。
よって,△OPCを回転させた方が体積が大きくなる。
PC=12/√5 に注意して,
V=(12/√5)^2×π×6/√5×1/3 という計算になる。
平成23年度・岡山県(数学)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・岡山県(数学)高校入試問題のダウンロードはこちらから
http://kenjukuren.moo.jp/QandA.htm
■■まとめ■■
問題がごちゃごちゃして,長い文章なのですが,読み解くとあっさり解ける問題が多かったです。[2][3][4]は図形の要素はあるものの,ほとんどが方程式を解くような問題ばかりで,出題がかなり偏っています。空間図形が1つもありませんでした。
■■解説■■
クリックすると大きくなります。参考にしてください。



■■ポイント■■
[1]計算と小問集合。
①~⑤計算すればよい。
⑥2(x+3)=(x-1)2 →2x+6=x2-2x+1→x2-4x-5=0 →(x-5)(x+1)=0。
よって,負の解はx=-1
⑦1次関数の公式に代入して,y=2(x-1)-3 → y=2x-5
⑧全部の場合の数は36通り。そのうち,目の積が奇数になるのは,(3,5),(5,3),(5,5)のみ。
⑨△BDCはBDが直径なので直角三角形である。円周角の定理より∠D=36°だから,∠B=54°
⑩ABの中点を作図するには,ABの垂直二等分線の作図をすればよい。
[2]方程式の問題
①全部で60ページだから,60-38-8=14ページ
②A~D班をxページとすると,E,F班はx+1ページになるので,4x+2(x+1)=14。
これを解くと,x=2。
[3]範囲が決まった関数。問題をよく読んで,条件を的確に当てはめること。
①絵里さんは,20枚のレポートだから,
12+6×20=132g。グラフを見るとア200円。また,240円で送るには,合計250g以下であれ
ばよいので,x枚のレポートを書いたとすると,12+6×x=250。x=39.… よってイ39枚
②条件Iより,絵里さんは200円だったから,一番少ないレポートの枚数(yとする)の場合,
12+6×y=100。→y=14.… となるので,最小は15枚のときである。また,最大は①で求め
た通り,合計39枚までだから,エ19枚までのとき,240円で送ることができる。
[4]周囲の長さによって面積がどう変わるか,という話。問題文が長いが,問題は簡単である。
①周の長さが12cmのとき,正六角形の1辺の長さはア2cm。正六角形の面積は図のように正三
角形6つ分と考える。1辺2の正三角形6枚分→√3/4 ×4×6=6√3
②[II]の証明は[I]と同様にやればよい。
9^2=81,(6√3)^2 で,81<108だから,9<6√3。
したがって,正方形の面積より,正六角形の面積が大きい。
③②より,面積が等しければ,正六角形の周の長さが一番短いことがわかる。するとハニカム
構造では,材料を少なくすることができる。
[5]同じ図の中で正多角形がいくつかある場合は,合同な図形ができやすいという問題。
①△APCと△BDCにおいて,
AC=BC(正三角形)…①
PC=DC(正三角形)…②
ここで,
∠ACP=60°-∠PCB
∠BCD=60°-∠PCB だから,
∠ACP=∠BCD…③
①,②,③より,2辺とその間の角がそれぞれ等しいので,△APC≡△BDC (証明終)
②PB^2+PC^2=PA^2のとき,
①よりPC=PD(イ),PA=DB(ア)であるから,代入すると,PB2+PD2=DB2(ウ)となる。
よって△PBDで三平方の定理の逆が成り立つので,∠BPD=90°である。
③PB=PC=2のとき,△PBCが二等辺三角形になることに気づくと速い。
まず,PB^2+PC^2=PA^2より,PA=2√2。
△PBCは二等辺三角形であり,∠BPC=150°だから∠PCB=15°。
よって,∠BCD=60-15=45°。BCの長さは,△CHDは45°定規で,CH=HD=√2 ,また,
BD=2√2 だから,△BHDは30°定規となり,BH=√6。
よって,BC=√2+√6EQ+QP+PC=(4-√3)+2×2√3=4+3√3
http://kenjukuren.moo.jp/QandA.htm
■■まとめ■■
問題がごちゃごちゃして,長い文章なのですが,読み解くとあっさり解ける問題が多かったです。[2][3][4]は図形の要素はあるものの,ほとんどが方程式を解くような問題ばかりで,出題がかなり偏っています。空間図形が1つもありませんでした。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]計算と小問集合。
①~⑤計算すればよい。
⑥2(x+3)=(x-1)2 →2x+6=x2-2x+1→x2-4x-5=0 →(x-5)(x+1)=0。
よって,負の解はx=-1
⑦1次関数の公式に代入して,y=2(x-1)-3 → y=2x-5
⑧全部の場合の数は36通り。そのうち,目の積が奇数になるのは,(3,5),(5,3),(5,5)のみ。
⑨△BDCはBDが直径なので直角三角形である。円周角の定理より∠D=36°だから,∠B=54°
⑩ABの中点を作図するには,ABの垂直二等分線の作図をすればよい。
[2]方程式の問題
①全部で60ページだから,60-38-8=14ページ
②A~D班をxページとすると,E,F班はx+1ページになるので,4x+2(x+1)=14。
これを解くと,x=2。
[3]範囲が決まった関数。問題をよく読んで,条件を的確に当てはめること。
①絵里さんは,20枚のレポートだから,
12+6×20=132g。グラフを見るとア200円。また,240円で送るには,合計250g以下であれ
ばよいので,x枚のレポートを書いたとすると,12+6×x=250。x=39.… よってイ39枚
②条件Iより,絵里さんは200円だったから,一番少ないレポートの枚数(yとする)の場合,
12+6×y=100。→y=14.… となるので,最小は15枚のときである。また,最大は①で求め
た通り,合計39枚までだから,エ19枚までのとき,240円で送ることができる。
[4]周囲の長さによって面積がどう変わるか,という話。問題文が長いが,問題は簡単である。
①周の長さが12cmのとき,正六角形の1辺の長さはア2cm。正六角形の面積は図のように正三
角形6つ分と考える。1辺2の正三角形6枚分→√3/4 ×4×6=6√3
②[II]の証明は[I]と同様にやればよい。
9^2=81,(6√3)^2 で,81<108だから,9<6√3。
したがって,正方形の面積より,正六角形の面積が大きい。
③②より,面積が等しければ,正六角形の周の長さが一番短いことがわかる。するとハニカム
構造では,材料を少なくすることができる。
[5]同じ図の中で正多角形がいくつかある場合は,合同な図形ができやすいという問題。
①△APCと△BDCにおいて,
AC=BC(正三角形)…①
PC=DC(正三角形)…②
ここで,
∠ACP=60°-∠PCB
∠BCD=60°-∠PCB だから,
∠ACP=∠BCD…③
①,②,③より,2辺とその間の角がそれぞれ等しいので,△APC≡△BDC (証明終)
②PB^2+PC^2=PA^2のとき,
①よりPC=PD(イ),PA=DB(ア)であるから,代入すると,PB2+PD2=DB2(ウ)となる。
よって△PBDで三平方の定理の逆が成り立つので,∠BPD=90°である。
③PB=PC=2のとき,△PBCが二等辺三角形になることに気づくと速い。
まず,PB^2+PC^2=PA^2より,PA=2√2。
△PBCは二等辺三角形であり,∠BPC=150°だから∠PCB=15°。
よって,∠BCD=60-15=45°。BCの長さは,△CHDは45°定規で,CH=HD=√2 ,また,
BD=2√2 だから,△BHDは30°定規となり,BH=√6。
よって,BC=√2+√6EQ+QP+PC=(4-√3)+2×2√3=4+3√3
平成23年度・長野県(数学)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・長野県(数学)高校入試問題のダウンロードはこちらから
http://www.pref.nagano.lg.jp/kyouiku/kyougaku/koukounuusi/index23.htm
■■まとめ■■
かなり難しい問題が入っています。関数の最後のほうは関数を図形的に考えることのできる力や,図形の最後の問題はかなり難しかったことでしょう。点数が取れる問題から取り組むことが大切です。
■■解説■■
クリックすると大きくなります。参考にしてください。



■■ポイント■■
[1]小問集合
(1)計算問題→難なくこなしてほしいところ。
(2)x2+2x=6x+12 → x2-4x-12=0 因数分解して(x-6)(x+2)=0 → x=6,-2
(3)全体aを5bずつ配ると,3個余るので,a=5b+3
(4)反比例の一般式はxy=aとも書ける。比例定数aは,-3×2=-6。よって,-9y=-6。
(5)作図問題。中心はABCからの距離が等しい点であるから,垂直二等分線の作図をする。
AとBから,BとCからの垂直二等分線を2回作図した交点が中心である。
(6)面積が等しい,というキーワードが出てきたときは,平行線を引く,という手順を
覚えておく。△AOB=△AOPであるから,AOは固定させておき,Bを動かす。
図のようにBからAOに平行な線を引き,Aからx軸に平行な線との交点がPになる。
OAの傾きは-1,B(2,4)であるから,直線BPはy=-x+6で,Pのy座標は1だからP(5,1)
(7)△EAF∽△EBCで,相似比は2:5であるから,AFの長さは16/5。よってFD=8-16/5=24/5
[2]いろいろな問題
(1)①Pは真下,Qは右側にあるので,弧PQは円周の1/4になっているから,円周角は45°
②まず,全部の場合の数は4×3=12通り。
∠A=90°のときは,PQが直径になる。(1,3),(3,1)のときの2通りになる。
③丁寧に考える。Pが1のときは・・・と,順番にやる。
P=1のとき,(x,y)=(1,3),(1,4)
P=2のとき,(x,y)=(2,4)
P=3のとき,(x,y)=(3,1),(3,4)
P=4のとき,(x,y)=(4,1),(4,2),(4,3) よって,合計8通りになる。
(2)タイルの数を数えると,n番目で必要なタイルはn2である。
①6番目は62=36枚
②方程式を作ると,n2+47=(n+1)2となる。これを解くと,n=23となる。
(3)問題用紙の絵が多少みにくいが,頂点Aに集まるすべての角が90°であることに注意する。
①△ABCを底面とすると,高さはADとなる。
②体積を2通りで見る方法である
① 底面△ABC,高さAD
② 底面△BCD,高さx
△BCDの長さを求めると,△ABC,△ACDは3:4:5の直角三角形であるからBC=CD=5。
△ABDは45°定規になっているので,BD=4√2。よって図でBH=2√2。
ここから,三平方の定理より,CH=√17となるので,体積を2通りで見ればよい。
[3]ダイヤグラムの問題
(1)弟は鉄塔まで30分で歩いたので,2100÷30=70(m/秒)
(2)姉の速さは60m/秒であるから,傾きは-60。また(70,0)を通るので,
y=-6(x-70)=-60x+4200
(3)①弟は70分後に,100mの地点にいたことになる。弟は(30,2100)と(70,100)を通るので,
傾きは-50。よって,弟の直線の式はy=-50(x-70)+100=-50x+3600。
y=0となるとき,x=72より,2分後
②t分後にこのことが起こったとすると,
-50t+3600=-60(t+1)+4200
※姉が1分後に弟と同じ距離のところになるという式
これを解くと,t=54であり,-50×54+3600=900(m)
(4)弟が姉より早く着くには,姉と同時に到着するよりも早ければよい。つまり,(30,2100)
と(70,0)を通ればよいので,このときの速さはア52.5(m/分)とすればよい。(ただし,姉
よりも遅い速さで弟が動いたので,b<60である。)
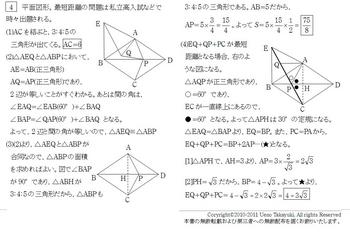
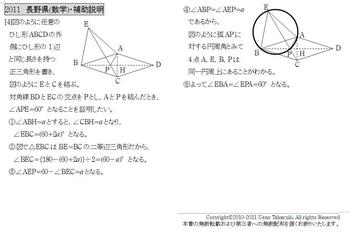
[4]平面図形。最短距離の問題は私立高入試などで時々出題される。
(1)ACを結ぶと,3:4:5の三角形が出てくる。AC=6
(2)△AEQと△ABPにおいて,
AE=AB(正三角形)
AQ=AP(正三角形)であり,
2辺が等しいことがすぐわかる。あとは間の角は,
∠EAQ=∠EAB(60°)+∠BAQ
∠BAP=∠QAP(60°)+∠BAQ となる。
よって,2辺と間の角が等しいので,△AEQ≡△ABP
(3)(2)より,△AEQと△ABPが合同なので,△ABPの面積を求めればよい。
∠BAPが90°であり,△ABHが3:4:5の三角形だから,△ABPも3:4:5の三角形である。
AB=5だから,AP=5×3/4=15/4 。よってS=5×15/4×1/2=75/8
(4)EQ+QP+PCが最短距離となる場合,図のようになる。
△AQPが正三角形であり,○=60°であり,
ECが一直線上にあるので,●=60°となる。よって△APHは30°の定規になる。
△EAQ=△BAPより,EQ=BP。また,PC=PAから,
EQ+QP+PC=BP+2AP…(★)となる。
[1]△APHで,AH=3より,AP=2√3
[2]PH=√3だから,BP=4-√3。よって★より,
EQ+QP+PC=(4-√3)+2×2√3=4+3√3
■■補助説明■■
クリックすると大きくなります。参考にしてください。
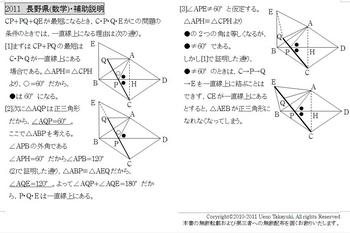
http://www.pref.nagano.lg.jp/kyouiku/kyougaku/koukounuusi/index23.htm
■■まとめ■■
かなり難しい問題が入っています。関数の最後のほうは関数を図形的に考えることのできる力や,図形の最後の問題はかなり難しかったことでしょう。点数が取れる問題から取り組むことが大切です。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]小問集合
(1)計算問題→難なくこなしてほしいところ。
(2)x2+2x=6x+12 → x2-4x-12=0 因数分解して(x-6)(x+2)=0 → x=6,-2
(3)全体aを5bずつ配ると,3個余るので,a=5b+3
(4)反比例の一般式はxy=aとも書ける。比例定数aは,-3×2=-6。よって,-9y=-6。
(5)作図問題。中心はABCからの距離が等しい点であるから,垂直二等分線の作図をする。
AとBから,BとCからの垂直二等分線を2回作図した交点が中心である。
(6)面積が等しい,というキーワードが出てきたときは,平行線を引く,という手順を
覚えておく。△AOB=△AOPであるから,AOは固定させておき,Bを動かす。
図のようにBからAOに平行な線を引き,Aからx軸に平行な線との交点がPになる。
OAの傾きは-1,B(2,4)であるから,直線BPはy=-x+6で,Pのy座標は1だからP(5,1)
(7)△EAF∽△EBCで,相似比は2:5であるから,AFの長さは16/5。よってFD=8-16/5=24/5
[2]いろいろな問題
(1)①Pは真下,Qは右側にあるので,弧PQは円周の1/4になっているから,円周角は45°
②まず,全部の場合の数は4×3=12通り。
∠A=90°のときは,PQが直径になる。(1,3),(3,1)のときの2通りになる。
③丁寧に考える。Pが1のときは・・・と,順番にやる。
P=1のとき,(x,y)=(1,3),(1,4)
P=2のとき,(x,y)=(2,4)
P=3のとき,(x,y)=(3,1),(3,4)
P=4のとき,(x,y)=(4,1),(4,2),(4,3) よって,合計8通りになる。
(2)タイルの数を数えると,n番目で必要なタイルはn2である。
①6番目は62=36枚
②方程式を作ると,n2+47=(n+1)2となる。これを解くと,n=23となる。
(3)問題用紙の絵が多少みにくいが,頂点Aに集まるすべての角が90°であることに注意する。
①△ABCを底面とすると,高さはADとなる。
②体積を2通りで見る方法である
① 底面△ABC,高さAD
② 底面△BCD,高さx
△BCDの長さを求めると,△ABC,△ACDは3:4:5の直角三角形であるからBC=CD=5。
△ABDは45°定規になっているので,BD=4√2。よって図でBH=2√2。
ここから,三平方の定理より,CH=√17となるので,体積を2通りで見ればよい。
[3]ダイヤグラムの問題
(1)弟は鉄塔まで30分で歩いたので,2100÷30=70(m/秒)
(2)姉の速さは60m/秒であるから,傾きは-60。また(70,0)を通るので,
y=-6(x-70)=-60x+4200
(3)①弟は70分後に,100mの地点にいたことになる。弟は(30,2100)と(70,100)を通るので,
傾きは-50。よって,弟の直線の式はy=-50(x-70)+100=-50x+3600。
y=0となるとき,x=72より,2分後
②t分後にこのことが起こったとすると,
-50t+3600=-60(t+1)+4200
※姉が1分後に弟と同じ距離のところになるという式
これを解くと,t=54であり,-50×54+3600=900(m)
(4)弟が姉より早く着くには,姉と同時に到着するよりも早ければよい。つまり,(30,2100)
と(70,0)を通ればよいので,このときの速さはア52.5(m/分)とすればよい。(ただし,姉
よりも遅い速さで弟が動いたので,b<60である。)
[4]平面図形。最短距離の問題は私立高入試などで時々出題される。
(1)ACを結ぶと,3:4:5の三角形が出てくる。AC=6
(2)△AEQと△ABPにおいて,
AE=AB(正三角形)
AQ=AP(正三角形)であり,
2辺が等しいことがすぐわかる。あとは間の角は,
∠EAQ=∠EAB(60°)+∠BAQ
∠BAP=∠QAP(60°)+∠BAQ となる。
よって,2辺と間の角が等しいので,△AEQ≡△ABP
(3)(2)より,△AEQと△ABPが合同なので,△ABPの面積を求めればよい。
∠BAPが90°であり,△ABHが3:4:5の三角形だから,△ABPも3:4:5の三角形である。
AB=5だから,AP=5×3/4=15/4 。よってS=5×15/4×1/2=75/8
(4)EQ+QP+PCが最短距離となる場合,図のようになる。
△AQPが正三角形であり,○=60°であり,
ECが一直線上にあるので,●=60°となる。よって△APHは30°の定規になる。
△EAQ=△BAPより,EQ=BP。また,PC=PAから,
EQ+QP+PC=BP+2AP…(★)となる。
[1]△APHで,AH=3より,AP=2√3
[2]PH=√3だから,BP=4-√3。よって★より,
EQ+QP+PC=(4-√3)+2×2√3=4+3√3
■■補助説明■■
クリックすると大きくなります。参考にしてください。
平成23年度・愛知県B(数学)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・愛知県B(数学)高校入試問題のダウンロードはこちらから
●私塾につながりますので,リンク先は明示いたしません。ご了承ください。
■■まとめ■■
図形の問題で考えさせるものが入っているのは例年通りです。相似,相似比と体積比に関する問題も出題されています。また,A問題と似ている問題(グラフの交点を求める)がありました。図形の最後は考えにくい問題も含まれていたと思います。
■■解説■■
クリックすると大きくなります。参考にしてください。

■■ポイント■■
[1]小問集合。
[1]小問集合。
(1)~(4) 計算問題
(5)(x+4y)(x-4y)+6xy=x2+6xy-16y2=(x+8y)(x-2y)
(6)x2-7x+8=0 これは因数分解できそうに見えるができないので,解の公式で解く。
(7)y=ax2でxがpからqまで変化するときの変化の割合は,a(p+q)で表せる。
[2]小問集合。
(1)Aさんの所持金をa,Bさんの所持金をbとして,連立方程式を作る。
よってAさんは3200円持っていた。
(2)半径が1/3 倍だから面積は1/9 倍。高さは5倍で,5/9倍
(3)①B(2,2)をy=ax2に代入すればいいので,2=4a。a=1/2
②△AOCの面積が△AOBの面積の2倍になるとき,OB=BCであるから,C(4,4)。
A(-4,8)より,直線ACの式を求める。
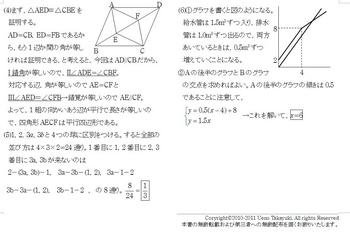
(4)まず,△AED≡△CBEを証明する。
AD=CB,ED=FBであるから,もう1辺か間の角が等しければ証明できる,と考えると,
今回はAD//CBだから,I錯角が等しいので,
II∠ADE=∠CBF。
対応する辺,角が等しいのでAE=CFとIII∠AED=∠CFB→錯覚が等しいのでAE//CF。
よって,1組の向かいあう辺が平行で長さが等しいので,四角形AECFは平行四辺形である。
(5)1,2,3a,3bと4つの球に区別をつける。すると全部の並び方は4×3×2=24通り。
1番目に1,2番目に2,3番目に3a,3bが来ないのは
2-(3a,3b)-1, 3a-3b-(1,2), 3a-1-2 3b-3a-(1,2), 3b-1-2 ,
の8通り。
(6)①グラフを書くと図のようになる。給水管は1.5m3ずつ入り,排水管は1.0m3ずつ出るので,
両方あいているときは,0.5m3ずつ増えていくことになる。
②Aの後半のグラフとBのグラフの交点を求めればよい。Aの後半のグラフの傾きは0.5である
ことに注意して,
{y=0.5(x-4)+8 →これを解いて,x=6
y=1.5x
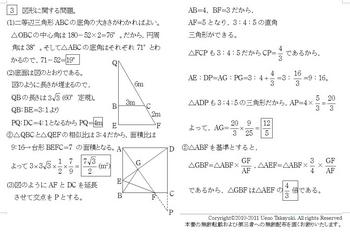
[3]図形に関する問題。
(1)二等辺三角形ABCの底角の大きさがわかればよい。△OBCの中心角は180-52×2=76°。だから,円周
角は38°。そして△ABCの底角はそれぞれ71°とわかるので,71-52=19°
(2)底面は図のとおりである。図のように長さが埋まるので,QBの長さは (60°定規)。
QB:BE=3:1よりPQ:DC=4:1となるからPQ=4m
②△QBCと△QEFの相似比は3:4だから,面積比は9:16→台形BEFC=7 の面積となる。
よって3×3√3×1/2×7/9=7√3/2 (m2)
(3)図のようにAFとDCを延長させて交点をPとする。
AB=4,BF=3だから,AF=5となり,3:4:5の直角三角形ができる。
△FCPも3:4:5だからCP=4/3であるから,AE:DP=AG:PG=3:4+4/3=9:16。
△ADPも3:4:5の三角形だから,AP=4×5/3=20/3。よって,AG=20/3×9/25=12/5
②△ABFを基準とすると,
△GBF=△ABF×GF/AF
△AEF=△ABF×3/4×GF/AFであるから,
△GBFは△AEFの4/3倍である。
●私塾につながりますので,リンク先は明示いたしません。ご了承ください。
■■まとめ■■
図形の問題で考えさせるものが入っているのは例年通りです。相似,相似比と体積比に関する問題も出題されています。また,A問題と似ている問題(グラフの交点を求める)がありました。図形の最後は考えにくい問題も含まれていたと思います。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]小問集合。
[1]小問集合。
(1)~(4) 計算問題
(5)(x+4y)(x-4y)+6xy=x2+6xy-16y2=(x+8y)(x-2y)
(6)x2-7x+8=0 これは因数分解できそうに見えるができないので,解の公式で解く。
(7)y=ax2でxがpからqまで変化するときの変化の割合は,a(p+q)で表せる。
[2]小問集合。
(1)Aさんの所持金をa,Bさんの所持金をbとして,連立方程式を作る。
よってAさんは3200円持っていた。
(2)半径が1/3 倍だから面積は1/9 倍。高さは5倍で,5/9倍
(3)①B(2,2)をy=ax2に代入すればいいので,2=4a。a=1/2
②△AOCの面積が△AOBの面積の2倍になるとき,OB=BCであるから,C(4,4)。
A(-4,8)より,直線ACの式を求める。
(4)まず,△AED≡△CBEを証明する。
AD=CB,ED=FBであるから,もう1辺か間の角が等しければ証明できる,と考えると,
今回はAD//CBだから,I錯角が等しいので,
II∠ADE=∠CBF。
対応する辺,角が等しいのでAE=CFとIII∠AED=∠CFB→錯覚が等しいのでAE//CF。
よって,1組の向かいあう辺が平行で長さが等しいので,四角形AECFは平行四辺形である。
(5)1,2,3a,3bと4つの球に区別をつける。すると全部の並び方は4×3×2=24通り。
1番目に1,2番目に2,3番目に3a,3bが来ないのは
2-(3a,3b)-1, 3a-3b-(1,2), 3a-1-2 3b-3a-(1,2), 3b-1-2 ,
の8通り。
(6)①グラフを書くと図のようになる。給水管は1.5m3ずつ入り,排水管は1.0m3ずつ出るので,
両方あいているときは,0.5m3ずつ増えていくことになる。
②Aの後半のグラフとBのグラフの交点を求めればよい。Aの後半のグラフの傾きは0.5である
ことに注意して,
{y=0.5(x-4)+8 →これを解いて,x=6
y=1.5x
[3]図形に関する問題。
(1)二等辺三角形ABCの底角の大きさがわかればよい。△OBCの中心角は180-52×2=76°。だから,円周
角は38°。そして△ABCの底角はそれぞれ71°とわかるので,71-52=19°
(2)底面は図のとおりである。図のように長さが埋まるので,QBの長さは (60°定規)。
QB:BE=3:1よりPQ:DC=4:1となるからPQ=4m
②△QBCと△QEFの相似比は3:4だから,面積比は9:16→台形BEFC=7 の面積となる。
よって3×3√3×1/2×7/9=7√3/2 (m2)
(3)図のようにAFとDCを延長させて交点をPとする。
AB=4,BF=3だから,AF=5となり,3:4:5の直角三角形ができる。
△FCPも3:4:5だからCP=4/3であるから,AE:DP=AG:PG=3:4+4/3=9:16。
△ADPも3:4:5の三角形だから,AP=4×5/3=20/3。よって,AG=20/3×9/25=12/5
②△ABFを基準とすると,
△GBF=△ABF×GF/AF
△AEF=△ABF×3/4×GF/AFであるから,
△GBFは△AEFの4/3倍である。
平成23年度・愛知県A(数学)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・愛知県A(数学)高校入試問題のダウンロードはこちらから
●私塾につながりますので,リンク先は明示いたしません。ご了承ください。
※[3](1)確率の問題の解き方を間違えていましたので,訂正しました。(3/11 2:00)
■■まとめ■■
図形の問題で考えさせるものが入っているのは例年通りです。相似,相似比と体積比に関する問題も出題されていますので,そのあたりをよく復習しておきましょう。全体的にやっておいた方がいい問題ばかりです。
■■解説■■
クリックすると大きくなります。参考にしてください。



■■ポイント■■
[1]小問集合。
(1)~(4)は特に問題ないだろう。
(5)2a+3×6=8bとなる。よって,移項して2で割ると,a=4b-9
(6)(x-2)2=x+4 → x-4x+4=x+4 → x2-5x=0 → x(x-5)=0 よって,x=0,5
(7)このような平方根の数の大小は,すべてを2乗して比べればよい。
すべて2乗すると,ア26,イ25,ウ24で,エは49/2=24.5となる。
よって,最大はア,最小はウ
[2]いろいろな問題。
(1)2次関数の変域の問題は,0を通過するときに十分に注意する。今回はx軸よりも下に
グラフがあるので,最小値はx=3のときの,y=-3。よって,0≦y≦-3
(2)花子さんは結局15分かかって学校についた。
A地点までの距離をx(m)として,
x/100+(1200-x)/60=15。これを解くと,x=750mである。
(3)Pから垂線を立てる作図は,
これは△QAPと△QBPが合同になることを利用したものである。
PA=PB,PQ=PQ,AQ=アBQであるから,
3辺が等しいので,△QAP≡△QBP
よって, ∠QPA=イ∠QPB
ここで,∠QPA+∠QPB=ウ180°から,∠QPA=90°
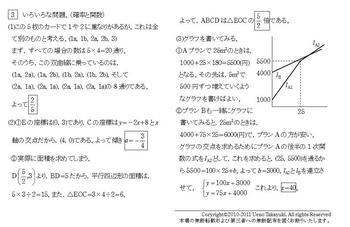
[3]いろいろな問題。(確率と関数)
(1)この5枚のカードで1や2に重なりがあるが,これは全て別のものと考える。(1a,1b,2a,2b,3)
まず,すべての場合の数は5×4=20通り。そのうち,この双曲線に乗っているのは,
(1a,2a),(1a,2b),(1b,2a),(1b,2b),そして
(2a,1a),(2a,1a),(2a,1a),(2a,1a)の8通りである。
よって8/20=2/5
(2)①Eの座標は(0,3)であり,Cの座標はy=-2x+8とx軸の交点だから,(4,0)である。
よって傾きa=-3/4
②実際に面積を求めてしまう。
D(5/2,3)より,BD=5だから,平行四辺形の面積は,5×3÷2=15。また,△EOC=3×4÷2=6。
よって,ABCDは△EOCの5/2倍である。
(3)グラフを書いてみる。
①Aプランで25m3のときは,1000+25×180=5500(円) となる。その先は,5m3で500円ずつ増
えていくようなグラフを書けばよい。
②プランBも一緒にグラフに書いてみると,25m3のときは,4000+75×25=6000(円)で,プラン
Aの方が安い。グラフの交点を求めるためにプランAの後半の1次関数の式をlA2として,
これを求めると,
(25,5500)を通るから5500=100×25+b。よってb=3000。
lA2とlBを連立させて,
①y=100x+3000
②y=75x+4000 これより,x=40。
[4]図形に関する問題。
(1)内角の和で攻める。
あ.△DCFの内角の和より,∠CDF=38°。
い.∠ADC=90°だから,∠DEF=26°。
う.△EDFは二等辺三角形だから,∠EFD=77°
よって,∠EFB=51°。
(2)OE=5,EC=7だから,半径12である。
①∠CDAは大きな弧ABCの円周角である。中心角が270°であるから,円周角は135°。
②直角三角形EOBに注目すると,EO=5,OB=12だから,EB=13となって,ピタゴラス数の三角形に
なっている。角Bが共通であるから,△ADB∽△EOBであり,△ADBは5:12:13の辺の比を
もつ。よって,AB=24であることに注意して,AD=24×5/13=120/13
(3)空間の比(相似比と面積比,体積比)に関する問題。
①図Iの水の入った上面(Pとする)の面積が12cm2で,Pと面BECDとの相似比が1:2であるから,
面積比は1:4。つまり,面BCDE=48cm2である。
よってV=48×3×1/3=128cm3
②図Iの水の入った部分は全体の体積の何倍か。
水の入っていない小さな四角すい:全体の四角すいの相似比が1:2であるから,体積比は
1:8。つまり,水の入った部分の体積は全体の7/8である。
図IIを見ると,結局底面の台形の面積は四角形BCDEの7/8になっていればよい。
①より,底面BCDE=48cm2だったから,底面の1辺の長さは4√3,B+FEがCB+DEの7/8になる
には,DF:FE=1:3となればよい。よってFE=3√3(cm)
●私塾につながりますので,リンク先は明示いたしません。ご了承ください。
※[3](1)確率の問題の解き方を間違えていましたので,訂正しました。(3/11 2:00)
■■まとめ■■
図形の問題で考えさせるものが入っているのは例年通りです。相似,相似比と体積比に関する問題も出題されていますので,そのあたりをよく復習しておきましょう。全体的にやっておいた方がいい問題ばかりです。
■■解説■■
クリックすると大きくなります。参考にしてください。
■■ポイント■■
[1]小問集合。
(1)~(4)は特に問題ないだろう。
(5)2a+3×6=8bとなる。よって,移項して2で割ると,a=4b-9
(6)(x-2)2=x+4 → x-4x+4=x+4 → x2-5x=0 → x(x-5)=0 よって,x=0,5
(7)このような平方根の数の大小は,すべてを2乗して比べればよい。
すべて2乗すると,ア26,イ25,ウ24で,エは49/2=24.5となる。
よって,最大はア,最小はウ
[2]いろいろな問題。
(1)2次関数の変域の問題は,0を通過するときに十分に注意する。今回はx軸よりも下に
グラフがあるので,最小値はx=3のときの,y=-3。よって,0≦y≦-3
(2)花子さんは結局15分かかって学校についた。
A地点までの距離をx(m)として,
x/100+(1200-x)/60=15。これを解くと,x=750mである。
(3)Pから垂線を立てる作図は,
これは△QAPと△QBPが合同になることを利用したものである。
PA=PB,PQ=PQ,AQ=アBQであるから,
3辺が等しいので,△QAP≡△QBP
よって, ∠QPA=イ∠QPB
ここで,∠QPA+∠QPB=ウ180°から,∠QPA=90°
[3]いろいろな問題。(確率と関数)
(1)この5枚のカードで1や2に重なりがあるが,これは全て別のものと考える。(1a,1b,2a,2b,3)
まず,すべての場合の数は5×4=20通り。そのうち,この双曲線に乗っているのは,
(1a,2a),(1a,2b),(1b,2a),(1b,2b),そして
(2a,1a),(2a,1a),(2a,1a),(2a,1a)の8通りである。
よって8/20=2/5
(2)①Eの座標は(0,3)であり,Cの座標はy=-2x+8とx軸の交点だから,(4,0)である。
よって傾きa=-3/4
②実際に面積を求めてしまう。
D(5/2,3)より,BD=5だから,平行四辺形の面積は,5×3÷2=15。また,△EOC=3×4÷2=6。
よって,ABCDは△EOCの5/2倍である。
(3)グラフを書いてみる。
①Aプランで25m3のときは,1000+25×180=5500(円) となる。その先は,5m3で500円ずつ増
えていくようなグラフを書けばよい。
②プランBも一緒にグラフに書いてみると,25m3のときは,4000+75×25=6000(円)で,プラン
Aの方が安い。グラフの交点を求めるためにプランAの後半の1次関数の式をlA2として,
これを求めると,
(25,5500)を通るから5500=100×25+b。よってb=3000。
lA2とlBを連立させて,
①y=100x+3000
②y=75x+4000 これより,x=40。
[4]図形に関する問題。
(1)内角の和で攻める。
あ.△DCFの内角の和より,∠CDF=38°。
い.∠ADC=90°だから,∠DEF=26°。
う.△EDFは二等辺三角形だから,∠EFD=77°
よって,∠EFB=51°。
(2)OE=5,EC=7だから,半径12である。
①∠CDAは大きな弧ABCの円周角である。中心角が270°であるから,円周角は135°。
②直角三角形EOBに注目すると,EO=5,OB=12だから,EB=13となって,ピタゴラス数の三角形に
なっている。角Bが共通であるから,△ADB∽△EOBであり,△ADBは5:12:13の辺の比を
もつ。よって,AB=24であることに注意して,AD=24×5/13=120/13
(3)空間の比(相似比と面積比,体積比)に関する問題。
①図Iの水の入った上面(Pとする)の面積が12cm2で,Pと面BECDとの相似比が1:2であるから,
面積比は1:4。つまり,面BCDE=48cm2である。
よってV=48×3×1/3=128cm3
②図Iの水の入った部分は全体の体積の何倍か。
水の入っていない小さな四角すい:全体の四角すいの相似比が1:2であるから,体積比は
1:8。つまり,水の入った部分の体積は全体の7/8である。
図IIを見ると,結局底面の台形の面積は四角形BCDEの7/8になっていればよい。
①より,底面BCDE=48cm2だったから,底面の1辺の長さは4√3,B+FEがCB+DEの7/8になる
には,DF:FE=1:3となればよい。よってFE=3√3(cm)
平成23年度・埼玉県前期(数学)高校入試問題 [平成23年度(2011年)・数学]
平成23年度・埼玉県(数学)高校入試問題のダウンロードはこちらから
http://www.tokyo-np.co.jp/k-shiken/index.html
■■まとめ■■
[1]の小問,[2]の小問で[3][4]は大問という構成は例年通りです。
[4]はとっつきにくかったのではないでしょうか。
★★[4](2)は求めたい長さをxをおいて,そのあとどのように式を作るか,ということが問われました。(3)は長方形であることを見抜いて欲しい問題でした。
■■ポイント■■
[1]小問集合
[1]計算問題。
(1)問題ないだろう。
(2)問題ないだろう。
(3)√45-2√5=3√5-2√5=√5
(4)x2-6x-16=(x-8)(x+2)と式変形できるので,ここでx=18を代入して,10×20=200
(5)2次方程式の解の公式を使う。
(6)これも問題ないだろう。
(7)2次関数の変化の割合の公式a(p+q)を使って,1/2×(1+5)=a。よってa=3
(8)相似比と体積比の問題。
体積比:全体8に対して上側の1をもらうから,
体積比8:1 → 相似比2:1となる。
つまり,上から4cmのところで切ればよい。
(9)△ABCで∠B+∠C=180-48=132°。辺BD,辺CDはそれぞれ角の二等分線なので,
△DBCで∠B+∠C=132÷2=66°。△DBCの内角の和を考えて,180-66=114°
(10)まずは全部の場合は6×6×6=216通り。
ア.同じ方向にまわり続ける場合 (6,6,6)のみ黒石がPに戻れる。
イ.偶数と奇数が出る場合は,3回の出た目の和が0になればよいが,偶数が2回
出てしまっては0に戻ることはできないので,偶数によって場合分けする。
a) (2,○,○)の場合,3回で(2,-1,-1) が出ればよい。
あとはこの並べ替え方を考えて3通り。
b) (4,○,○)の場合,3回で(4,-1,-3) が出ればよい。
あとはこの並べ替え方を考えて6通り。
c) (6,○,○)の場合,3回で(6,-3,-3)か(6,-1,-5)
(6,-3,-3)は a)の考え方で3通り。
(6,-1,-5)は b)の考え方で6通り。よって,合計19通りある。
(11)方程式などを作らずに,割り算をして考える。
ア.①電球が2個あるので,合計3時間使う。よって,12÷3=4日分
②1日3時間テレビを見るので,1週間では21時間分。よって,21÷3=7個
イ.車いすは24000円。
これに必要なアルミ缶の重さは24000÷100=240kg
これに必要なアルミ缶の個数は240kg÷15g=16000個
全校生徒320人なので,16000÷320=50個
10か月で目標を達成するから,50÷10=5個
[2]小問集合
(1)樹形図を書いて丁寧に考える。
(2)図3の重なった点をPとして,Pから垂線PQを下ろすと,△CAB∽△CPQだから,
PQ=12/5。求める面積は△ABC+△BDC-△PBC。あとは計算する。
(3)直角三角形の1通りめは,Aからy軸に垂線を下した場合でP(0,3)。
2通りめはOA⊥APとなる場合で,O(0,0),A(3,3)だから,P(0,6)となる。
(4)①まずは直線OPを引く。
②次にPから垂線を立てる作図をする。
[3]数式の性質に関する問題。(2)は県発表の解答と別の方法でやってみる。
(1)3(2n+1)=32×52 → 2n+1=3×25=75
よって,2n=74だから,n=37。
3つの奇数は2n-1,2n+1,2n+3だから,73,75,77
(2)5つの奇数をn-4,n-2,n,n+2,n+4とすると,この5つの奇数の和は5nとなる。
だから,√5nが整数になるには,nが5×p2という形になればよいが,そもそもnは
奇数でなければならないので,その最小値はp=1のとき。次に小さいときはp=3の
ときで,その場合のnは45。よって,41,43,45,47,49
[4]平面図形に関する問題。ちょっと最後が難しいか。
(1)この相似は折れ線90°の形としてよく出てくる形である。
△EBFと△FCBにおいて
長方形ABCDの性質より
∠B=∠C=90°……①
長方形EFGHで∠F=90°だから,
∠EFB+∠GFC=90°……②
また,△GFCは直角三角形だから,
∠FGC+∠GFC=90°……③
②・③より,
∠EFB=∠FGC ……④
①・④より,2角がそれぞれ等しいので,
△EBF∽△FCG (証明終)
(2)まずEFGHであるが,面積が半分,ということは,実は全体のABCDをADとCBが重なる
ように半分に折った形と全く同じであることに注意したい。
すると,AD=12,AB=12√2,EF=12,GF=6√2となる。
求めたいBF=xとすると,CF=12-xであり,△EBFと△FCGは相似比√2:1だから,
EB=√2(12-x) 。
よって,△EBFで三平方の定理より,
x^2+{√2(12-x)}^2=12^2。
x^2+2(144-24x+x^2)=144 → 3x^2-48x+144=0
→ x^2-16x+48=0 →(x-12)(x-4)=0 x=12はあり得ないので,x=BF=4
(3)なんとなくEIJLが長方形であることが見えるか?
それが説明できればあとは難しくない。
①ア)まず(1)の証明より,∠EFB+∠GFC=90°で,折り曲げを考えると,∠EFI+JFC=90°
だから,FIとFJは一直線上に並ぶ。
イ)アと同様に∠FGC+∠HGD=90°だから,∠JGF+∠JGK=90°となり,GJとGLは一直線上
にある。
ウ)∠B=∠EIF=90°,∠C=∠GJF=90°,∠D=∠KLG=90°だから,四角形EIJLは長方形
である。
②EI=EB=8√2,FG=FJ=8,BF=FI=4だから,IJ=4
よって,S=8√2×4=32√2 となる。
http://www.tokyo-np.co.jp/k-shiken/index.html
■■まとめ■■
[1]の小問,[2]の小問で[3][4]は大問という構成は例年通りです。
[4]はとっつきにくかったのではないでしょうか。
★★[4](2)は求めたい長さをxをおいて,そのあとどのように式を作るか,ということが問われました。(3)は長方形であることを見抜いて欲しい問題でした。
■■ポイント■■
[1]小問集合
[1]計算問題。
(1)問題ないだろう。
(2)問題ないだろう。
(3)√45-2√5=3√5-2√5=√5
(4)x2-6x-16=(x-8)(x+2)と式変形できるので,ここでx=18を代入して,10×20=200
(5)2次方程式の解の公式を使う。
(6)これも問題ないだろう。
(7)2次関数の変化の割合の公式a(p+q)を使って,1/2×(1+5)=a。よってa=3
(8)相似比と体積比の問題。
体積比:全体8に対して上側の1をもらうから,
体積比8:1 → 相似比2:1となる。
つまり,上から4cmのところで切ればよい。
(9)△ABCで∠B+∠C=180-48=132°。辺BD,辺CDはそれぞれ角の二等分線なので,
△DBCで∠B+∠C=132÷2=66°。△DBCの内角の和を考えて,180-66=114°
(10)まずは全部の場合は6×6×6=216通り。
ア.同じ方向にまわり続ける場合 (6,6,6)のみ黒石がPに戻れる。
イ.偶数と奇数が出る場合は,3回の出た目の和が0になればよいが,偶数が2回
出てしまっては0に戻ることはできないので,偶数によって場合分けする。
a) (2,○,○)の場合,3回で(2,-1,-1) が出ればよい。
あとはこの並べ替え方を考えて3通り。
b) (4,○,○)の場合,3回で(4,-1,-3) が出ればよい。
あとはこの並べ替え方を考えて6通り。
c) (6,○,○)の場合,3回で(6,-3,-3)か(6,-1,-5)
(6,-3,-3)は a)の考え方で3通り。
(6,-1,-5)は b)の考え方で6通り。よって,合計19通りある。
(11)方程式などを作らずに,割り算をして考える。
ア.①電球が2個あるので,合計3時間使う。よって,12÷3=4日分
②1日3時間テレビを見るので,1週間では21時間分。よって,21÷3=7個
イ.車いすは24000円。
これに必要なアルミ缶の重さは24000÷100=240kg
これに必要なアルミ缶の個数は240kg÷15g=16000個
全校生徒320人なので,16000÷320=50個
10か月で目標を達成するから,50÷10=5個
[2]小問集合
(1)樹形図を書いて丁寧に考える。
(2)図3の重なった点をPとして,Pから垂線PQを下ろすと,△CAB∽△CPQだから,
PQ=12/5。求める面積は△ABC+△BDC-△PBC。あとは計算する。
(3)直角三角形の1通りめは,Aからy軸に垂線を下した場合でP(0,3)。
2通りめはOA⊥APとなる場合で,O(0,0),A(3,3)だから,P(0,6)となる。
(4)①まずは直線OPを引く。
②次にPから垂線を立てる作図をする。
[3]数式の性質に関する問題。(2)は県発表の解答と別の方法でやってみる。
(1)3(2n+1)=32×52 → 2n+1=3×25=75
よって,2n=74だから,n=37。
3つの奇数は2n-1,2n+1,2n+3だから,73,75,77
(2)5つの奇数をn-4,n-2,n,n+2,n+4とすると,この5つの奇数の和は5nとなる。
だから,√5nが整数になるには,nが5×p2という形になればよいが,そもそもnは
奇数でなければならないので,その最小値はp=1のとき。次に小さいときはp=3の
ときで,その場合のnは45。よって,41,43,45,47,49
[4]平面図形に関する問題。ちょっと最後が難しいか。
(1)この相似は折れ線90°の形としてよく出てくる形である。
△EBFと△FCBにおいて
長方形ABCDの性質より
∠B=∠C=90°……①
長方形EFGHで∠F=90°だから,
∠EFB+∠GFC=90°……②
また,△GFCは直角三角形だから,
∠FGC+∠GFC=90°……③
②・③より,
∠EFB=∠FGC ……④
①・④より,2角がそれぞれ等しいので,
△EBF∽△FCG (証明終)
(2)まずEFGHであるが,面積が半分,ということは,実は全体のABCDをADとCBが重なる
ように半分に折った形と全く同じであることに注意したい。
すると,AD=12,AB=12√2,EF=12,GF=6√2となる。
求めたいBF=xとすると,CF=12-xであり,△EBFと△FCGは相似比√2:1だから,
EB=√2(12-x) 。
よって,△EBFで三平方の定理より,
x^2+{√2(12-x)}^2=12^2。
x^2+2(144-24x+x^2)=144 → 3x^2-48x+144=0
→ x^2-16x+48=0 →(x-12)(x-4)=0 x=12はあり得ないので,x=BF=4
(3)なんとなくEIJLが長方形であることが見えるか?
それが説明できればあとは難しくない。
①ア)まず(1)の証明より,∠EFB+∠GFC=90°で,折り曲げを考えると,∠EFI+JFC=90°
だから,FIとFJは一直線上に並ぶ。
イ)アと同様に∠FGC+∠HGD=90°だから,∠JGF+∠JGK=90°となり,GJとGLは一直線上
にある。
ウ)∠B=∠EIF=90°,∠C=∠GJF=90°,∠D=∠KLG=90°だから,四角形EIJLは長方形
である。
②EI=EB=8√2,FG=FJ=8,BF=FI=4だから,IJ=4
よって,S=8√2×4=32√2 となる。



